Advertisements
Advertisements
प्रश्न
Prove the following by using the principle of mathematical induction for all n ∈ N: 1.2 + 2.22 + 3.22 + … + n.2n = (n – 1) 2n+1 + 2
उत्तर
Let the given statement be P(n), i.e.,
P(n): 1.2 + 2.22 + 3.22 + … + n.2n = (n – 1) 2n+1 + 2
For n = 1, we have
P(1): 1.2 = 2 = (1 – 1) 21+1 + 2 = 0 + 2 = 2, which is true.
Let P(k) be true for some positive integer k, i.e.,
1.2 + 2.22 + 3.22 + … + k.2k = (k – 1) 2k + 1 + 2 … (i)
We shall now prove that P(k + 1) is true.
Consider
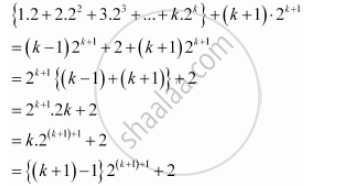
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
APPEARS IN
संबंधित प्रश्न
Prove the following by using the principle of mathematical induction for all n ∈ N:
Prove the following by using the principle of mathematical induction for all n ∈ N:
Prove the following by using the principle of mathematical induction for all n ∈ N:
(1+3/1)(1+ 5/4)(1+7/9)...`(1 + ((2n + 1))/n^2) = (n + 1)^2`
Prove the following by using the principle of mathematical induction for all n ∈ N: `1+2+ 3+...+n<1/8(2n +1)^2`
If P (n) is the statement "n2 + n is even", and if P (r) is true, then P (r + 1) is true.
1 + 2 + 3 + ... + n = \[\frac{n(n + 1)}{2}\] i.e. the sum of the first n natural numbers is \[\frac{n(n + 1)}{2}\] .
\[\frac{1}{3 . 5} + \frac{1}{5 . 7} + \frac{1}{7 . 9} + . . . + \frac{1}{(2n + 1)(2n + 3)} = \frac{n}{3(2n + 3)}\]
1.2 + 2.22 + 3.23 + ... + n.2n = (n − 1) 2n+1+2
1.2 + 2.3 + 3.4 + ... + n (n + 1) = \[\frac{n(n + 1)(n + 2)}{3}\]
32n+7 is divisible by 8 for all n ∈ N.
52n+2 −24n −25 is divisible by 576 for all n ∈ N.
32n+2 −8n − 9 is divisible by 8 for all n ∈ N.
11n+2 + 122n+1 is divisible by 133 for all n ∈ N.
7 + 77 + 777 + ... + 777 \[{. . . . . . . . . . .}_{n - \text{ digits } } 7 = \frac{7}{81}( {10}^{n + 1} - 9n - 10)\]
\[\frac{(2n)!}{2^{2n} (n! )^2} \leq \frac{1}{\sqrt{3n + 1}}\] for all n ∈ N .
Show by the Principle of Mathematical induction that the sum Sn of then terms of the series \[1^2 + 2 \times 2^2 + 3^2 + 2 \times 4^2 + 5^2 + 2 \times 6^2 + 7^2 + . . .\] is given by \[S_n = \binom{\frac{n \left( n + 1 \right)^2}{2}, \text{ if n is even} }{\frac{n^2 \left( n + 1 \right)}{2}, \text{ if n is odd } }\]
\[\text{ A sequence } a_1 , a_2 , a_3 , . . . \text{ is defined by letting } a_1 = 3 \text{ and } a_k = 7 a_{k - 1} \text{ for all natural numbers } k \geq 2 . \text{ Show that } a_n = 3 \cdot 7^{n - 1} \text{ for all } n \in N .\]
\[\text { A sequence } x_1 , x_2 , x_3 , . . . \text{ is defined by letting } x_1 = 2 \text{ and } x_k = \frac{x_{k - 1}}{k} \text{ for all natural numbers } k, k \geq 2 . \text{ Show that } x_n = \frac{2}{n!} \text{ for all } n \in N .\]
\[\text{ The distributive law from algebra states that for all real numbers} c, a_1 \text{ and } a_2 , \text{ we have } c\left( a_1 + a_2 \right) = c a_1 + c a_2 . \]
\[\text{ Use this law and mathematical induction to prove that, for all natural numbers, } n \geq 2, if c, a_1 , a_2 , . . . , a_n \text{ are any real numbers, then } \]
\[c\left( a_1 + a_2 + . . . + a_n \right) = c a_1 + c a_2 + . . . + c a_n\]
Prove by method of induction, for all n ∈ N:
2 + 4 + 6 + ..... + 2n = n (n+1)
Prove by method of induction, for all n ∈ N:
12 + 22 + 32 + .... + n2 = `("n"("n" + 1)(2"n" + 1))/6`
Prove by method of induction, for all n ∈ N:
13 + 33 + 53 + .... to n terms = n2(2n2 − 1)
Prove by method of induction, for all n ∈ N:
`1/(3.5) + 1/(5.7) + 1/(7.9) + ...` to n terms = `"n"/(3(2"n" + 3))`
Prove by method of induction, for all n ∈ N:
(24n−1) is divisible by 15
Answer the following:
Prove, by method of induction, for all n ∈ N
`1/(3.4.5) + 2/(4.5.6) + 3/(5.6.7) + ... + "n"/(("n" + 2)("n" + 3)("n" + 4)) = ("n"("n" + 1))/(6("n" + 3)("n" + 4))`
Answer the following:
Prove by method of induction 152n–1 + 1 is divisible by 16, for all n ∈ N.
Answer the following:
Prove by method of induction 52n − 22n is divisible by 3, for all n ∈ N
The distributive law from algebra says that for all real numbers c, a1 and a2, we have c(a1 + a2) = ca1 + ca2.
Use this law and mathematical induction to prove that, for all natural numbers, n ≥ 2, if c, a1, a2, ..., an are any real numbers, then c(a1 + a2 + ... + an) = ca1 + ca2 + ... + can.
State whether the following proof (by mathematical induction) is true or false for the statement.
P(n): 12 + 22 + ... + n2 = `(n(n + 1) (2n + 1))/6`
Proof By the Principle of Mathematical induction, P(n) is true for n = 1,
12 = 1 = `(1(1 + 1)(2*1 + 1))/6`. Again for some k ≥ 1, k2 = `(k(k + 1)(2k + 1))/6`. Now we prove that
(k + 1)2 = `((k + 1)((k + 1) + 1)(2(k + 1) + 1))/6`
Give an example of a statement P(n) which is true for all n. Justify your answer.
Prove the statement by using the Principle of Mathematical Induction:
n2 < 2n for all natural numbers n ≥ 5.
Prove the statement by using the Principle of Mathematical Induction:
2n < (n + 2)! for all natural number n.
A sequence a1, a2, a3 ... is defined by letting a1 = 3 and ak = 7ak – 1 for all natural numbers k ≥ 2. Show that an = 3.7n–1 for all natural numbers.
If P(n): 2n < n!, n ∈ N, then P(n) is true for all n ≥ ______.
