Advertisements
Advertisements
Question
Should the energy of a photon be called its kinetic energy or its internal energy?
Solution
Relativistic equation of energy :
`E^2 = p^2c^2 + m^2c^4` ....(1)
Here, p2c2 = kinetic energy of photon
m02c4 = internal energy of photon
We know photons have zero rest mass. Therefore, m0 = 0. Substituting the value of m0 = 0 in equation (1), we get : `E = pc`
Thus, the energy of a photon should be called its kinetic energy.
APPEARS IN
RELATED QUESTIONS
Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?
The following graph shows the variation of photocurrent for a photosensitive metal :
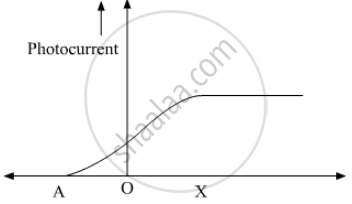
(a) Identify the variable X on the horizontal axis.
(b) What does the point A on the horizontal axis represent?
(c) Draw this graph for three different values of frequencies of incident radiation v1, v2 and v3 (v1 > v2 > v3) for same intensity.
(d) Draw this graph for three different values of intensities of incident radiation I1, I2 and I3 (I1 > I2 > I3) having same frequency.
It is found that yellow light does not eject photoelectrons from a metal. Is it advisable to try with orange light or with green light?
If an electron has a wavelength, does it also have a colour?
A photon of energy hv is absorbed by a free electron of a metal with work-function hv − φ.
In which of the following situations, the heavier of the two particles has smaller de Broglie wavelength? The two particles
(a) move with the same speed
(b) move with the same linear momentum
(c) move with the same kinetic energy
(d) have fallen through the same height
A parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflecting plane mirror. The angle of incidence is 60° and the number of photons striking the mirror per second is 1.0 × 1019. Calculate the force exerted by the light beam on the mirror.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A sphere of radius 1.00 cm is placed in the path of a parallel beam of light of large aperture. The intensity of the light is 0.5 W cm−2. If the sphere completely absorbs the radiation falling on it, find the force exerted by the light beam on the sphere.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
The electric field associated with a light wave is given by `E = E_0 sin [(1.57 xx 10^7 "m"^-1)(x - ct)]`. Find the stopping potential when this light is used in an experiment on photoelectric effect with the emitter having work function 1.9 eV.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A small piece of cesium metal (φ = 1.9 eV) is kept at a distance of 20 cm from a large metal plate with a charge density of 1.0 × 10−9 C m−2 on the surface facing the cesium piece. A monochromatic light of wavelength 400 nm is incident on the cesium piece. Find the minimum and maximum kinetic energy of the photoelectrons reaching the large metal plate. Neglect any change in electric field due to the small piece of cesium present.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Define the term: threshold frequency

On the basis of the graphs shown in the figure, answer the following questions :
(a) Which physical parameter is kept constant for the three curves?
(b) Which is the highest frequency among v1, v2, and v3?
Consider a thin target (10–2 cm square, 10–3 m thickness) of sodium, which produces a photocurrent of 100 µA when a light of intensity 100W/m2 (λ = 660 nm) falls on it. Find the probability that a photoelectron is produced when a photons strikes a sodium atom. [Take density of Na = 0.97 kg/m3].
The work function for a metal surface is 4.14 eV. The threshold wavelength for this metal surface is ______.
The graph shows the variation of photocurrent for a photosensitive metal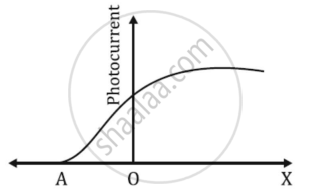
- What does X and A on the horizontal axis represent?
- Draw this graph for three different values of frequencies of incident radiation ʋ1, ʋ2 and ʋ3 (ʋ3 > ʋ2 > ʋ1) for the same intensity.
- Draw this graph for three different values of intensities of incident radiation I1, I2 and I3 (I3 > I2 > I1) having the same frequency.
Why it is the frequency and not the intensity of the light source that determines whether the emission of photoelectrons will occur or not? Explain.
How would the stopping potential for a given photosensitive surface change if the frequency of the incident radiation were increased? Justify your answer.
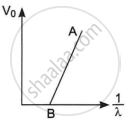
The figure shows a plot of stopping potential (V0) versus `1/lambda`, where λ is the wavelength of the radiation causing photoelectric emission from a surface. The slope of the line is equal to ______.
Plot a graph showing the variation of photoelectric current, as a function of anode potential for two light beams having the same frequency but different intensities I1 and I2 (I1 > I2). Mention its important features.
