Advertisements
Advertisements
Question
State basic proportionality theorem and its converse.
Solution
TO STATE: The basic proportionality theorem and its converse.
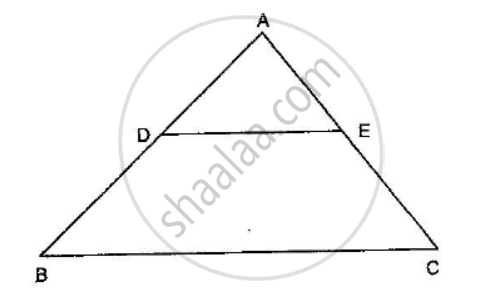
BASIC PROPORTIONALITY THEOREM: If a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
CONVERSE OF BASIC PROPORTIONALITY THEOREM: If a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
APPEARS IN
RELATED QUESTIONS
In the below figure, If AB || CD, find the value of x.
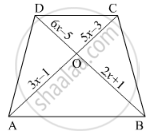
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
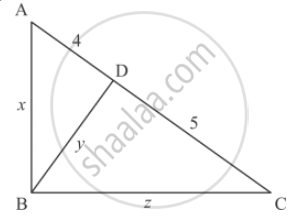
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
In the given figure, DE || BC and \[AD = \frac{1}{2}BD\]. If BC = 4.5 cm, find DE.
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
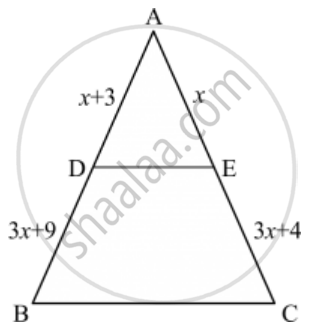
In the given figure, the value of x for which DE || AB is