Advertisements
Advertisements
Question
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at ______.
Options
`(3(2 + b))/(4(3 + b))`
`(4(2 + b))/(3(3 + b))`
`(3(3 + b))/(4(2 + b))`
`(4(3 + b))/(3(2 + b))`
Solution
The density of a non-uniform rod of length 1 m is given by ρ(x) = a(1 + bx2) where a and b are constants and 0 ≤ x ≤ 1. The centre of mass of the rod will be at `underline((3(2 + b))/(4(3 + b)))`.
Explanation:
Density is given as ρ(x) = a(1 + bx2)
Where a and b are constant and 0 ≤ x ≤ 1
Let b → 0, in this case ρ(x) = a = constant
Hence, the centre of mass will be at x = 0.5 m. (middle of the rod)
Putting b = 0 in all the options, only (a) gives 0.5.
APPEARS IN
RELATED QUESTIONS
If all the particles of a system lie in X-Y plane, is it necessary that the centre of mass be in X-Y plane?
If all the particle of a system lie in a cube, is it necessary that the centre of mass be in the cube?
You are holding a cage containing a bird. Do you have to make less effort if the bird flies from its position in the cage and manages to stay in the middle without touching the walls of the cage? Does it makes a difference whether the cage is completely closed or it has rods to let air pass?
A high-jumper successfully clears the bar. Is it possible that his centre of mass crossed the bar from below it? Try it with appropriate figures.
In an elastic collision
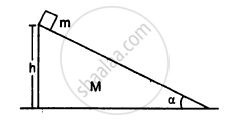
A block of mass m is placed on a triangular block of mass M which in turn is placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
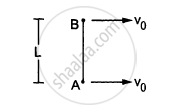
Two small balls A and B, each of mass m, are joined rigidly to the ends of a light rod of length L (see the following figure). The system translates on a frictionless horizontal surface with a velocity \[\nu_0\] in a direction perpendicular to the rod. A particle P of mass m kept at rest on the surface sticks to the ball A as the ball collides with it. Find
(a) the linear speeds of the balls A and B after the collision, (b) the velocity of the centre of mass C of the system A + B + P and (c) the angular speed of the system about C after the collision.
[Hint : The light rod will exert a force on the ball B
only along its length.]
A round object of mass M and radius R rolls down without slipping along an inclined plane. The frictional force, ______
Define centre of mass.
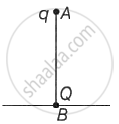
A point charge Q is situated at point B on the ground. A point charge q of mass m is vertically dropped along line AB from a multi-storey building of height h. Find the position of the point charge q when it is in equilibrium.