Advertisements
Advertisements
Question
The marks obtained by 200 students in an examination are given below :
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No.of students | 5 | 10 | 11 | 20 | 27 | 38 | 40 | 29 | 14 | 6 |
Using a graph paper, draw an Ogive for the above distribution. Use your Ogive to estimate:
(i) the median;
(ii) the lower quartile;
(iii) the number of students who obtained more than 80% marks in the examination and
(iv) the number of students who did not pass, if the pass percentage was 35.
Use the scale as 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis.
Solution 1
We construct cumulative frequency table of the given distribution :
| Marks | No. of students (f) | Cumulative Frequency |
| 0-10 | 5 | 5 |
| 10-20 | 10 | 15 |
| 20-30 | 11 | 26 |
| 30-40 | 20 | 46 |
| 40-50 | 27 | 73 |
| 50-60 | 38 | 111 |
| 60-70 | 40 | 151 |
| 70-80 | 29 | 180 |
| 80-90 | 14 | 194 |
| 90-100 | 6 | 200 |
Take a graph paper and draw both the axes.
On the x - axis , take a scale of 1cm= 20 to represent the marks.
On the y - axis , take a scale of 1 cm =50 to represent the no. of students.
Now, plot the points (10 ,5) ,(20 ,15) ,(30 ,26) ,( 40 ,46) ,(50 ,73) ,(60 ,111), (70 ,151) ,(80 ,180) ,(90 ,194) ,(100 ,200) .
Join them by a smooth curve to get the ogive.

(i) No. of terms = 200
∴ Median = `(100 + 101)/2` = 100.5th term
Through mark of 100.5 on y-axis draw a line parallel to x-axis which meets the curve at A. From A, draw a perpendicular to x-axis which meets it at B.
The value of B is the median which is 58.5.
(ii) Lower Quartile (Q1) = `n/4 = 200/4` = 50th term
Through mark of 50 on y-axis draw a line parallel to x-axis which meets the curve at P. From P, draw a perpendicular to x-axis which meets it at Q.
The value of Q is the lower quartile which is 41 .
(iii) From marks = 80 draw a line parallel to y-axis and meet the curve at R. From R, Draw a perpendicular on y-axis which meets it at S. The difference of the value obtained when subtracted from 200 gives the number of students who scored more than 80%.
⇒ 200 - 180 = 20
20 students scored more than 80%
Solution 2
| Less than | C.F. | Points |
| 10 | 5 | (10, 5) |
| 20 | 15 | (20, 15) |
| 30 | 26 | (30, 26) |
| 40 | 46 | (40, 46) |
| 50 | 73 | (50, 73) |
| 60 | 111 | (60, 111) |
| 70 | 151 | (70, 151) |
| 80 | 180 | (80, 180) |
| 90 | 194 | (90, 194) |
| 100 | 200 | (100, 200) |
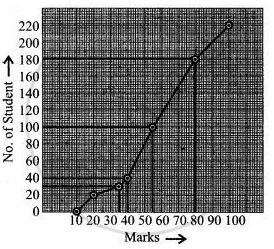
(i) Median = `"N"/(2) = (200)/(2)`
= 100 → On seeing the corresponding value.
Median = 57
(ii) Q1 = `"N"/(4) = (200)/(4)`
= 50 → On seeing the corresponding value.
= 38
(iii) 200 - 180 = 20 students
(iv) 38 students did not pass.
APPEARS IN
RELATED QUESTIONS
The ages of 40 students are given in the following table :
| Age (in years) | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Frequency | 2 | 4 | 6 | 9 | 8 | 7 | 4 |
Find the arithmetic mean.
If the mean of the following observations is 54, find the value of p.
| Class | 0 – 20 | 20 – 40 | 40 – 60 | 60 – 80 | 80 – 100 |
| Frequency | 7 | p | 10 | 9 | 13 |
By drawing an ogive, estimate the median for the following frequency distribution:
| Weight (kg) | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 | 30 – 35 |
| No. of boys | 11 | 25 | 12 | 5 | 2 |
The marks of 20 students in a test were as follows:
2, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19 and 20.
Calculate:
- the mean
- the median
- the mode
What is the median of 7, 10, 7, 5, 9, 10?
Find the mean of all numbers from 7 to 17.
Find the mean of the following frequency distribution by the short cut method :
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 9 | 12 | 15 | 10 | 14 |
Find the mode of the following:
15, 17, 16, 17, 10, 12, 14, 16, 19, 12, 16, 15, 16
In 10 numbers, arranged in increasing order, the 7th number is increased by 8, how much will the median be changed?
Find the mean and the median of: 5, 8, 10, 11,13, 16, 19 and 20
