Advertisements
Advertisements
Question
The number of road accidents in the city due to rash driving, over a period of 3 years, is given in the following table:
| Year | Jan-March | April-June | July-Sept. | Oct.-Dec. |
| 2010 | 70 | 60 | 45 | 72 |
| 2011 | 79 | 56 | 46 | 84 |
| 2012 | 90 | 64 | 45 | 82 |
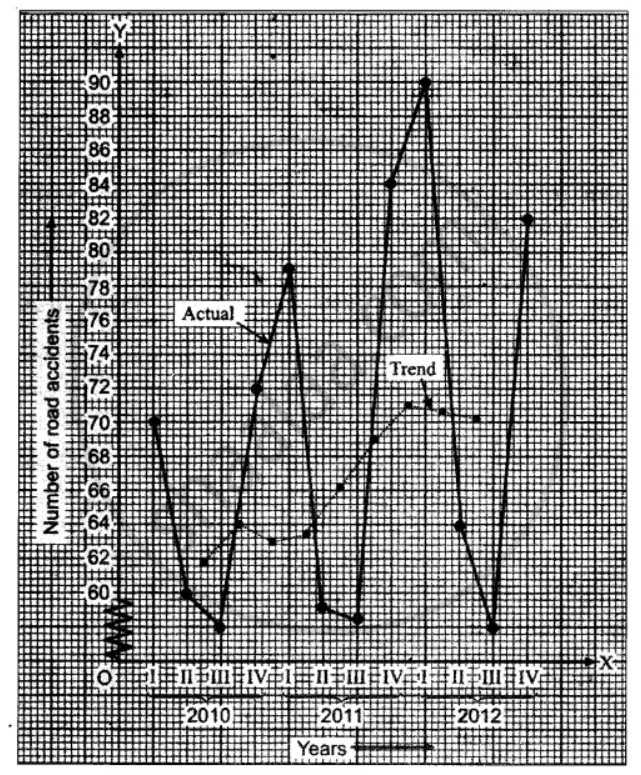
Calculate four quarterly moving averages and illustrate them and original figures on one graph using the same axes for both.
Solution
| Year/Quarters | Road Accidents | 4 quarterly moving total | 4 quarterly moving average |
|
`{:(I), (II), (III), (IV):}}2010` |
70 60 45 72 |
247 |
61.75 |
| Year/Quarters | Road Accidents | 4 quarterly moving total | 4 quarterly moving average |
|
`{:(I), (II), (III), (IV):}}2011` |
79 56 46 84 |
252 253 265 276 |
63 |
|
`{:(I), (II), (III), (IV):}}2012` |
90 64 45 82 |
284 283 281 |
71 |
APPEARS IN
RELATED QUESTIONS
If the function f(x)=2x3−9mx2+12m2x+1, where m>0 attains its maximum and minimum at p and q respectively such that p2=q, then find the value of m.
Differentiate tan2 x ?
Differentiate \[e^{\tan 3 x} \] ?
Differentiate \[x \sin 2x + 5^x + k^k + \left( \tan^2 x \right)^3\] ?
Differentiate \[\sin^2 \left\{ \log \left( 2x + 3 \right) \right\}\] ?
Prove that \[\frac{d}{dx} \left\{ \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2} \sin^{- 1} \frac{x}{a} \right\} = \sqrt{a^2 - x^2}\] ?
Differentiate \[\tan^{- 1} \left( \frac{2^{x + 1}}{1 - 4^x} \right), - \infty < x < 0\] ?
Differentiate \[\tan^{- 1} \left( \frac{a + bx}{b - ax} \right)\] ?
Differentiate \[\tan^{- 1} \left( \frac{5 x}{1 - 6 x^2} \right), - \frac{1}{\sqrt{6}} < x < \frac{1}{\sqrt{6}}\] ?
Differentiate the following with respect to x:
\[\cos^{- 1} \left( \sin x \right)\]
If the derivative of tan−1 (a + bx) takes the value 1 at x = 0, prove that 1 + a2 = b ?
If \[y \sqrt{1 - x^2} + x \sqrt{1 - y^2} = 1\] ,prove that \[\frac{dy}{dx} = - \sqrt{\frac{1 - y^2}{1 - x^2}}\] ?
Differentiate \[x^{\tan^{- 1} x }\] ?
Find \[\frac{dy}{dx}\] \[y = \left( \tan x \right)^{\log x} + \cos^2 \left( \frac{\pi}{4} \right)\] ?
Find \[\frac{dy}{dx}\] ,When \[x = a \left( 1 - \cos \theta \right) \text{ and } y = a \left( \theta + \sin \theta \right) \text{ at } \theta = \frac{\pi}{2}\] ?
If \[x = a \left( \theta - \sin \theta \right) and, y = a \left( 1 + \cos \theta \right), \text { find } \frac{dy}{dx} \text{ at }\theta = \frac{\pi}{3} \] ?
Differentiate x2 with respect to x3
Differentiate \[\sin^{- 1} \sqrt{1 - x^2}\] with respect to \[\cos^{- 1} x, \text { if}\]\[x \in \left( 0, 1 \right)\] ?
If \[y = x \left| x \right|\] , find \[\frac{dy}{dx} \text{ for } x < 0\] ?
If \[y = \tan^{- 1} \left( \frac{1 - x}{1 + x} \right), \text{ find} \frac{dy}{dx}\] ?
Differential coefficient of sec(tan−1 x) is ______.
\[\frac{d}{dx} \left\{ \tan^{- 1} \left( \frac{\cos x}{1 + \sin x} \right) \right\} \text { equals }\] ______________ .
If \[y = \sqrt{\sin x + y},\text { then } \frac{dy}{dx} =\] __________ .
If \[f\left( x \right) = \left| x^2 - 9x + 20 \right|\] then `f' (x)` is equal to ____________ .
Find the second order derivatives of the following function x3 log x ?
If x = a cos nt − b sin nt, then \[\frac{d^2 x}{d t^2}\] is
If \[f\left( x \right) = \frac{\sin^{- 1} x}{\sqrt{1 - x^2}}\] then (1 − x)2 f '' (x) − xf(x) =
f(x) = 3x2 + 6x + 8, x ∈ R
Find the height of a cylinder, which is open at the top, having a given surface area, greatest volume, and radius r.
