Advertisements
Advertisements
Question
The ratio between the interior angle and the exterior angle of a regular polygon is 2: 1. Find:
(i) each exterior angle of the polygon ;
(ii) number of sides in the polygon.
Solution
Interior angle : exterior angle = 2 : 1
Let interior angle = 2x° & exterior angle = x°
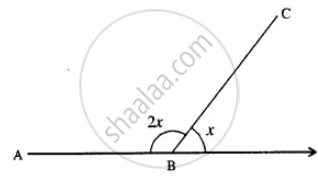
∴ 2x° + x° = 180°
3x = 180°
x = 60°
∴ Each exterior angle = 60°
Let no.of. sides = n
`(360°)/"n" = 60°`
n = `(360°)/(60°)`
n = 6
∴ (i) x = 60° (ii) 6
RELATED QUESTIONS
Fill in the blanks :
In case of regular polygon, with :
| No.of.sides | Each exterior angle | Each interior angle |
| (i) ___8___ | _______ | ______ |
| (ii) ___12____ | _______ | ______ |
| (iii) _________ | _____72°_____ | ______ |
| (iv) _________ | _____45°_____ | ______ |
| (v) _________ | __________ | _____150°_____ |
| (vi) ________ | __________ | ______140°____ |
Find the number of sides in a regular polygon, if its interior angle is: 160°
Find the number of sides in a regular polygon, if its interior angle is: `1 1/5` of a right angle
Find the number of sides in a regular polygon, if its exterior angle is: two-fifth of right angle
Is it possible to have a regular polygon whose interior angle is : 170°
The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. If each of the remaining exterior angles is x°, find the value of x.
The ratio between the number of sides of two regular polygons is 3 : 4 and the ratio between the sum of their interior angles is 2 : 3. Find the number of sides in each polygon.
Calculate the number of sides of a regular polygon, if: its interior angle is five times its exterior angle.
Calculate the number of sides of a regular polygon, if: its exterior angle exceeds its interior angle by 60°.
The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Find the number of sides in a regular polygon, if its interior angle is: 150°
Is it possible to have a regular polygon whose interior angle is: 135°
