Advertisements
Advertisements
Question
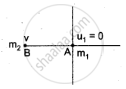
Two different unknown masses A and B collide. A is initially at rest when B has a speed v. After collision B has a speed v/2 and moves at right angles to its original direction of motion. Find the direction in which A moves after the collision.
Solution
Given:
`u_2 = v, u_1 = 0`
`v_2 = v/2, theta = ?`
Component along x-axis
`m_1v_1 costheta = m_2v` ..................(1)
Component along y-axis
`m_1v_1 sintheta = m_2(v/2)` ..................(2)
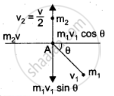
from (1) and (2)
`tan theta = ((v/2))/v = 1/2;`
`theta = tan^-1(1/2) = tan^-1(0.5); theta = 26^circ33^'.`
APPEARS IN
RELATED QUESTIONS
The rate of change of total momentum of a many-particle system is proportional to the ______ on the system.
Answer carefully, with reason:
If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy.)
The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table, as shown in the figure. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Solve the following problem.
A ball of mass 100 g dropped on the ground from 5 m bounces repeatedly. During every bounce, 64% of the potential energy is converted into kinetic energy. Calculate the following:
- Coefficient of restitution.
- The speed with which the ball comes up from the ground after the third bounce.
- The impulse was given by the ball to the ground during this bounce.
- Average force exerted by the ground if this impact lasts for 250 ms.
- The average pressure exerted by the ball on the ground during this impact if the contact area of the ball is 0.5 cm2.
Solve the following problem.
A spring ball of mass 0.5 kg is dropped from some height. On falling freely for 10 s, it explodes into two fragments of mass ratio 1:2. The lighter fragment continues to travel downwards with a speed of 60 m/s. Calculate the kinetic energy supplied during the explosion.
Solve the following problem.
A marble of mass 2m travelling at 6 cm/s is directly followed by another marble of mass m with double speed. After a collision, the heavier one travels with the average initial speed of the two. Calculate the coefficient of restitution.
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
In Rutherford experiment, for head-on collision of a-particles with a gold nucleus, the impact parameter is ______.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
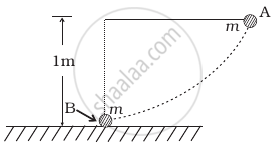
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
The dimension of mutual inductance is ______.
