Advertisements
Advertisements
Question
Using a graph paper, draw an ogive for the following distribution which shows a record of the width in kilograms of 200 students.
| Weight | Frequency |
| 40 – 45 | 5 |
| 45 – 50 | 17 |
| 50 – 55 | 22 |
| 55 – 60 | 45 |
| 60 – 65 | 51 |
| 65 – 70 | 31 |
| 70 – 75 | 20 |
| 75 – 80 | 9 |
Use your ogive to estimate the following:
- The percentage of student weighting 55 kg or more
- The weight above which the heaviest 30% of the student fall
- The number of students who are
- underweight
- overweight, If 55.70 kg is considered as standard weight.
Solution
| Weight | Frequency | C.f |
| 40 – 45 | 5 | 5 |
| 45 – 50 | 17 | 22 |
| 50 – 55 | 22 | 44 |
| 55 – 60 | 45 | 89 |
| 60 – 65 | 51 | 140 |
| 65 – 70 | 31 | 171 |
| 70 – 75 | 20 | 191 |
| 75 – 80 | 9 | 200 |
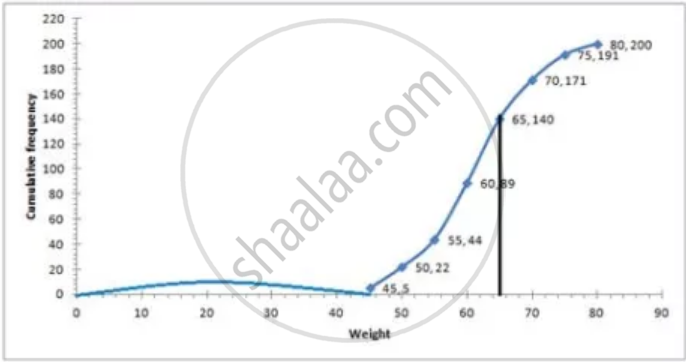
i. Number of students weighing more than 55 kg = 200 – 44 = 156
Therefore, percentage of students weighing 55 kg or more
= `156/200 xx 100`
= 78%
ii. 30% of students = `(30 xx 200)/100 = 60`
Heaviest 60 students in weight = 9 + 21 + 30 = 60
Weight = 65 kg ...(From table)
iii. a. underweight students when 55.70 kg is standard = 46 (approx) from graph
b. overweight student when 55.70 kg is standard = 200 – 46 = 154 (approx) from graph
APPEARS IN
RELATED QUESTIONS
- Find the mean of 7, 11, 6, 5 and 6.
- If each number given in (a) is diminished by 2; find the new value of mean.
By drawing an ogive, estimate the median for the following frequency distribution:
| Weight (kg) | 10 – 15 | 15 – 20 | 20 – 25 | 25 – 30 | 30 – 35 |
| No. of boys | 11 | 25 | 12 | 5 | 2 |
A boy scored following marks in various class tests during a term; each test being marked out of 20.
15, 17, 16, 7, 10, 12, 14, 16, 19, 12 and 16
What are his modal marks?
Find the mean of first 10 prime numbers.
Find the mean of the following frequency distribution :
| Class | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
| Frequency | 6 | 10 | 8 | 12 | 4 |
Find the median of the following:
25, 34, 31, 23, 22, 26, 35, 29, 20, 32
Find the median of:
241, 243, 347, 350, 327, 299, 261, 292, 271, 258 and 257
The mean of a certain number of observations is 32. Find the resulting mean, if the observation is, increased by 60%.
Find the median of 5, 7, 9, 11, 15, 17, 2, 23 and 19.
Find the mean of: all prime numbers upto 30
