Advertisements
Advertisements
Question
Verify each of the following:
(i)`sin 60^0 cos 30^0-cos 60^0 sin 30^0`
Solution
`sin 60^0 cos 30^0-cos 60^0 sin 30^0`
=`(sqrt(3)/2)xx(sqrt(3)/2) -(1/2)xx(1/2) = 3/4-1/4=2/4=1/2`
Also, `sin 30^0 =1/2`
∴ `sin 60^0 cos 30^0-cos 60^0 sin 30^0= sin 30^0`
APPEARS IN
RELATED QUESTIONS
If A = B = 60°. Verify `tan (A - B) = (tan A - tan B)/(1 + tan tan B)`
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
Prove that
cosec (65 °+ θ) sec (25° − θ) − tan (55° − θ) + cot (35° + θ) = 0
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
If cos A = `(1)/(2)` and sin B = `(1)/(sqrt2)`, find the value of: `(tan"A" – tan"B")/(1+tan"A" tan"B")`.
Are angles A and B from the same triangle? Explain.
In ΔABC, ∠B = 90°. If AB = 12units and BC = 5units, find: tan A
If cosec θ = `(29)/(20)`, find the value of: `("sec" θ)/("tan" θ - "cosec" θ)`
From the given figure, find the values of cosec C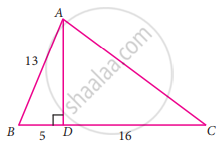
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
