Advertisements
Advertisements
Question
यदि `vec"a" + vec"b" + vec"c"` = 0, तो सिद्ध कीजिए कि `vec"a" xx vec"b" = vec"b" xx vec"c" = vec"c" xx vec"a"` इस परिणाम का ज्यामितीय विमोचन कीजिए।
Solution
दिया गया है कि `vec"a" + vec"b" + vec"c"` = 0
तो, `vec"a" xx (vec"a" + vec"b" + vec"c") = vec"a" xx 0`
⇒ `vec"a" xx vec"a" + vec"a" xx vec"b" + vec"a" xx vec"c"` = 0
⇒ `vec"0" + vec"a" xx vec"b" + vec"a" xx vec"c"` = 0 ....`(vec"a" xx vec"a" = 0)`
⇒ `vec"a" xx vec"b" - vec"c" xx vec"a"` = 0 ....`(vec"a" xx vec"c" = -vec"c" xx vec"a")`
⇒ `vec"a" xx vec"b" = vec"c" xx vec"a"` .....(i)
अब `vec"a" + vec"b" + vec"c"` = 0
⇒ `vec"b" xx (vec"a" + vec"b" + vec"c") = vec"b" xx 0`
⇒ `vec"b" xx vec"a" + vec"b" xx vec"b" xx vec"c"` = 0
⇒ `vec"b" xx vec"a" + vec0 + vec"b" xx vec"c"` = 0 ....`("क्योंकि" vec"b" xx vec"b" = 0)`
⇒ `-(vec"a" xx "b") + vec"b" xx vec"c"` = 0
∴ `vec"b" xx vec"c" = vec"a" xx vec"b"` ....(ii)
समीकरण (i) और (ii) से हम प्राप्त करते हैं
`vec"a" xx vec"b" = vec"b" xx vec"c" = vec"c" xx vec"a"`.
इसलिए साबित हुआ।
ज्यामितीय व्याख्या
आकृति के अनुसार, हम जानते हैं कि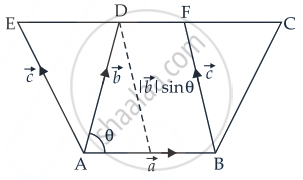
समांतर चतुर्भुज ABCD का क्षेत्रफल है।
⇒ `|vec"a" xx vec"b"| = |vec"a"||vec"b"| sin theta`
क्योंकि, एक ही आधार पर और एक ही समान्तर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
∴ `|vec"a" xx vec"b"| = |vec"b" xx vec"c"| = |vec"c" xx vec"a"|`
⇒ `vec"a" xx vec"b" xx vec"c" = vec"c" xx vec"a"`.
APPEARS IN
RELATED QUESTIONS
सदिशों `vec"a" = 2hat"i" - hat"j" + 2hat"k"` और `vec"b" = -hat"i" + hat"j" + 3hat"k"` के योग के अनुदिश मात्रक सदिश ज्ञात कीजिए।
यदि बिंदु (-1, -1, 2), (2, m, 5) और (3, 11, 6) सरेखी, हैं तो m का मान ज्ञात कीजिए।
परिमाण 3`sqrt2` का एक सदिश `vec"r"` ज्ञात कीजिए जो y और z-अक्षों से क्रमशः कोण `pi/4` और `pi/2` बनाता है।
सिद्ध कीजिए कि किसी ∆ABC, में `sin"A"/"a" = sin"B"/"b" = sin"C"/"c"`, जहाँ a, b, c क्रमश: A, B, C शीर्षों की सम्मुख भुजाओं के परिमाण को निरूपित करते हैं।
सदिश `6vec"i" + 2vec"j" + 3vec"k"` का परिमाण है
उस बिंदु का स्थिति सदिश, जो दो बिंदुओं, जिनके स्थिति सदिश क्रमश: `vec"a" + vec"b"` और 2`vec"a" + vec"b"` हैं, को 1:2 के अनुपात में विभाजित करता है,
यदि `|vec"a"| = 8, |vec"b"| = 3` और `|vec"a" xx vec"b"| = 12` है, तो `vec"a"*vec"b"` बराबर है
यदि `vec"a"` और `vec"b"` मात्रक सदिश हैं तो `sqrt(3) vec"a" - vec"b"` के मात्रक सदिश होने के लिए `vec"a"` और `vec"b"` के बीच क्या कोण होगा?
सदिश `vec"a" = 2hat"i" - hat"j" + hat"k"` और `vec"b" = 2hat"j" + hat"k"` के योग के अनुदिश मात्रक सदिश ज्ञात कीजिए।
यदि `vec"a" = hat"i" + hat"j" + 2hat"k"` और `hat"b" = 2hat"i" + hat"j" - 2hat"k"`, की दिशाओं में मात्रक सदिश है `2vec"a" - vec"b"`
सदिशों के प्रयोग से k का मान ज्ञात कीजिए ताकि बिंदु (k, -10, 3), (1, -1, 3) और(3, 5, 3) संरेखी हों।
एक सदिश `vec"r"` तीनों अक्षों से समान कोण पर झुका हुआ है। यदि `vec"r"` का परिमाण `2sqrt3` इकाई है तो `vec"r"` ज्ञात कीजिए।
परिमाण 6 का एक सदिश ज्ञात कीजिए जो दोनों ही सदिशों `2hat"i" - hat"j" + 2hat"k"` और `4hat"i" - hat"j" + 3hat"k"` पर लंब है।
सदिश दर `vec"a" = 3hat"i" + hat"j" + 2hat"k"` तथा सदिश `vec"b" = 2hat"i" - 2hat"j" + 4hat"k"` के बीच का sine ज्ञात कीजिए।
सदिशों के प्रयोग से त्रिभुज ABC का क्षेत्रफल ज्ञात कीजिए यदि जिसके शीर्ष A (1, 2, 3), B (2, -1, 4) और C (4, 5, -1) है।
सिद्ध कीजिए कि समांतर चतुर्भुज का क्षेत्रफल, जिसके विकर्ण `vec"a"` और `vec"b"` द्वारा व्यक्त हैं, `(|vec"a" xx vec"b"|)/2` है। साथ ही उस समांतर चतुर्भुज का क्षेत्रफल भी ज्ञात कीजिए जिसके विकर्ण `2hat"i" - hat"j" + hat"k"` और `hat"i" + 3hat"j" - hat"k"` है।
सदिश `hat"i" - 2hat"j" + 2hat"k"` की दिशा में परिमाण 9 वाला सदिश है
दो सदिशों `vec"a"` और `vec"b"` के परिमाण क्रमश: `sqrt(3)` और 4 हैं तथा `vec"a" * vec"b" = 2sqrt(3)` है। इनके बीच का कोण है
यदि सदिश `3hat"i" - 6hat"j" + hat"k"` और `2hat"i" - 4hat"j" + lambdahat"k"` समांतर हैं तो λ का मान है
मूल बिंदु से A और B बिंदुओं के सदिश क्रमश: `vec"a" = 2hat"i" - 3hat"j" + 2hat"k"` और `vec"b" = 2hat"i" + 3hat"j" + hat"k"`, हों तो त्रिभुज OAB का क्षेत्रफल है
यदि `|vec"a"|` = 10, `|vec"b"|` = 2 और `vec"a".vec"b"` = 12, हो तो `|vec"a" xx vec"b"|` का मान है
सदिश `vec"a"` का सदिश `vec"b"` पर प्रक्षेप
सदिशों `vec"a" = 2hat"i" + hat"j" + 2hat"k"` और `vec"b" = hat"j" + hat"k"` दोनों ही पर मात्रक लंब सदिशों की संख्या हैं
सदिश `vec"a" + vec"b"` असंरेखी सदिशों `vec"a"` और `vec"b"` के बीच के कोण को समद्विभाजित करता है यदि ______
यदि k के मानों के लिए `|"k"vec"a"| < |vec"a"|` और `"k"vec"a" + 1/2 vec"a"` सदिश `vec"a"` के समांतर है, तो k के मान ______ हैं।
व्यंजक `|vec"a" xx vec"b"|^2 + (vec"a".vec"b")^2` का मान ______ है।
