Advertisements
Advertisements
Find the derivative of `y = log x + 1/x` with respect to x.
Concept: Logarithmic Differentiation
The graph of the function f is shown below.
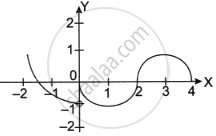
Of the following options, at what values of x is the function f NOT differentiable?
Concept: Concept of Continuity
Consider the graph `y = x^(1/3)`
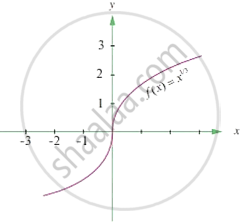
Statement 1: The above graph is continuous at x = 0
Statement 2: The above graph is differentiable at x = 0
Which of the following is correct?
Concept: Concept of Continuity
If xy = yx, then find `dy/dx`
Concept: Logarithmic Differentiation
If `y = (x + sqrt(a^2 + x^2))^m`, prove that `(a^2 + x^2)(d^2y)/(dx^2) + xdy/dx - m^2y = 0`
Concept: Derivatives of Composite Functions - Chain Rule
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is `6sqrt3` r.
Concept: Tangents and Normals
If the sum of the lengths of the hypotenuse and a side of a right triangle is given, show that the area of the triangle is maximum, when the angle between them is 60º.
Concept: Simple Problems on Applications of Derivatives
Find a point on the curve y = (x − 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Concept: Tangents and Normals
Find the approximate change in the volume ‘V’ of a cube of side x metres caused by decreasing the side by 1%.
Concept: Approximations
Find the points on the curve y = `4x^3 - 3x + 5` at which the equation of the tangent is parallel to the x-axis.
Concept: Tangents and Normals
Water is dripping out from a conical funnel of semi-verticle angle `pi/4` at the uniform rate of `2 cm^2/sec`in the surface, through a tiny hole at the vertex of the bottom. When the slant height of the water level is 4 cm, find the rate of decrease of the slant height of the water.
Concept: Increasing and Decreasing Functions
A cone is inscribed in a sphere of radius 12 cm. If the volume of the cone is maximum, find its height
Concept: Maximum and Minimum Values of a Function in a Closed Interval
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to \[ \frac{2}{3} \] of the diameter of the sphere.
Concept: Maxima and Minima
A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum the ratio of the length of the cylinder to the diameter of its semi-circular ends is \[\pi : (\pi + 2)\].
Concept: Maxima and Minima
Prove that the function `f(x) = x^3- 6x^2 + 12x+5` is increasing on R.
Concept: Increasing and Decreasing Functions
A 13 m long ladder is leaning against a wall, touching the wall at a certain height from the ground level. The bottom of the ladder is pulled away from the wall, along the ground, at the rate of 2 m/s. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall?
Concept: Rate of Change of Bodies or Quantities
The volume of a closed rectangular metal box with a square base is 4096 cm3. The cost of polishing the outer surface of the box is Rs. 4 per cm2. Find the dimensions of the box for the minimum cost of polishing it.
Concept: Maxima and Minima
Find the point on the straight line 2x+3y = 6, which is closest to the origin.
Concept: Maxima and Minima
A rectangle is inscribed in a semicircle of radius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get the maximum area. Also, find the maximum area.
Concept: Maxima and Minima
An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
Concept: Rate of Change of Bodies or Quantities
