Topics
Number System
Rational Numbers
- Rational Numbers
- Addition of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
- Rational Numbers on a Number Line
- Inserting Rational Numbers Between Two Given Rational Numbers
- Method of Finding a Large Number of Rational Numbers Between Two Given Rational Numbers
Exponents
- Concept of Exponents
- Law of Exponents (For Integral Powers)
- Negative Integral Exponents
- More About Exponents
Squares and Square Root
- Concept of Square Roots
- Finding Square Root by Division Method
- Finding Square Root Through Prime Factorisation
- To Find the Square Root of a Number Which is Not a Perfect Square (Using Division Method)
- Properties of Square Numbers
Cubes and Cube Roots
Playing with Numbers
- Arranging the Objects in Rows and Columns
- Generalized Form of Numbers
- Some Interesting Properties
- Letters for Digits (Cryptarithms)
- Divisibility by 10
- Divisibility by 2
- Divisibility by 5
- Divisibility by 3
- Divisibility by 6
- Divisibility by 11
- Divisibility by 4
Sets
- Concept of Sets
- Representation of a Set
- Cardinal Number of a Set
- Types of Sets
- Subset
- Proper Subset
- Number of Subsets and Proper Subsets of a Given Set
- Super Set
- Universal Set
- Complement of a Set
- Set Operations
- Difference of Two Sets
- Distributive Laws
- Venn Diagrams
Ratio and Proportion
Percent and Percentage
Profit, Loss and Discount
- Concept of Discount
- Overhead Expenses
- To Find S.P., When C.P. and Gain (Or Loss) Percent Are Given
- To Find C.P., When S.P. and Gain (Or Loss) Percent Are Given
- Concept of Discount
- Computation of Tax
- Goods and Service Tax (Gst)
- Gst Comprises of
Interest
- Calculation of Interest
- Concept of Compound Interest
- To Find the Principle (P); the Rate Percent (R) and the Time
- Interest Compounded Half Yearly
- Applications of Compound Interest Formula
Direct and Inverse Variations
- Variations
- Types of Variation
- Direct Variation
- Inverse Variation
- Concept for Unitary Method (With Only Direct Variation Implied)
- Concept of Arrow Method
- Time and Work
Algebra
Algebraic Expressions
- Algebraic Expressions
- Degree of Polynomial
- Product , Factor and Coefficient
- Like and Unlike Terms
- Combining like Terms
- Multiplying Monomial by Monomials
- Multiplying a Monomial by a Polynomial
- Multiplying a Polynomial by a Polynomial
- Dividing a Monomial by a Monomial
- Dividing a Polynomial by a Monomial
- Dividing a Polynomial by a Polynomial
- Simplification of Expressions
Identities
- Algebraic Identities
- Product of Sum and Difference of Two Terms
- Expansion Form of Numbers
- Important Formula of Expansion
- Cubes of Binomials
- Application of Formulae
Factorisation
- Factorisation by Taking Out Common Factors
- Factorisation by Taking Out Common Factors
- Factorisation by Grouping
- Factorisation by Difference of Two Squares
- Factorisation of Trinomials
- Factorising a Perfect Square Trinomial
- Factorising Completely
Linear Equations in One Variable
- Simple Linear Equations in One Variable
- Solving Linear Inequations
- Linear Equation in One Variable
- Equations Reducible to the Linear Form
Linear Inequations
- Introduction to linear equations in two variables
- Replacement Set and Solution Set
- Operation of Whole Numbers on Number Line
- Concept of Properties
Geometry
Understanding Shapes
- Different Types of Curves - Closed Curve, Open Curve, Simple Curve.
- Concept of Polygons
- Sum of Angles of a Polynomial
- Sum of Exterior Angles of a Polynomial
- Regular Polynomial
- Concept of Quadrilaterals
Special Types of Quadrilaterals
Constructions
- Introduction of Constructions
- Construction of an Angle
- To Construct an Angle Equal to Given Angle
- To Draw the Bisector of a Given Angle
- Construction of an angle bisector of an Angles of 60°,30°,90° and 45°
- Construction of Bisector of a Line
- The Perpendicular Bisector
- Construction of Parallel Lines
- Constructing a Quadrilateral
- Construction of Parallelograms
- Construction of a Rectangle When Its Length and Breadth Are Given.
- Construction of Rhombus
- Construction of Square
- Concept of Reflection Symmetry
Representing 3-D in 2-D
- 2dimensional Perspective of 3dimensional Objects
- Concept of Polyhedron
- Faces, Edges and Vertices
- Euler's Formula
- Concept of Polyhedron
- Nets for Building 3-d Shapes
Mensuration
Area of a Trapezium and a Polygon
Surface Area, Volume and Capacity
Data Handling (Statistics)
Data Handling
- Concept of Data Handling
- Collecting Data
- Frequency
- Raw Data, Arrayed Data and Frequency Distribution
- Constructing a Frequency Table
- Frequency Distribution Table
- Class Intervals and Class Limits
- Graphical Representation of Data
Probability
Notes
1. Whole Number on the number line:
A line that graphically represents the real numbers as a series of points whose distance from an origin is proportional to their value.
The distance between these points labelled as 0 and 1 is called unit distance.
A number written on the left-hand side of the number line is the smaller number and the number written on the right-hand side of the number line is the greater number.
We take a line, mark a point on it and label it 0. We then mark out points to the right of 0, at equal intervals. Label them as 1, 2, 3,... Thus, we have a number line with the whole numbers represented on it. We can easily perform the number operations of addition, subtraction, and multiplication on the number line.
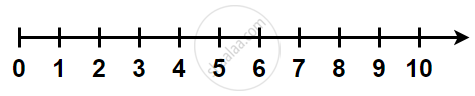
2. Operation on Number Line:
1) Addition on the number line:
Let us see the addition of 2 and 5.
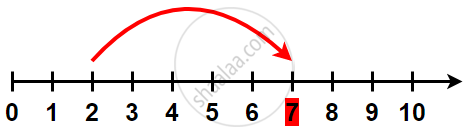
Start from 2. Then move 5 places to the right will give 7. The sum of 2 and 5 is 7, i.e. 2 + 5 = 7. Addition corresponds to moving to the right on the number line.
2) Subtraction on the number line:
Let us find 9 – 6.
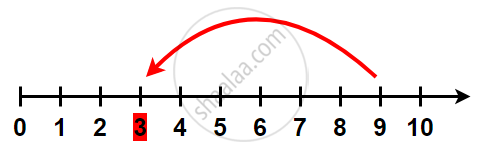
Start from 9. Since 6 is being subtracted, so move 6 places towards left will give 3. We get 7 – 5 = 2. Subtraction corresponds to moving to the left on the number line.
3) Multiplication on the number line:
Multiplication corresponds to making jumps of equal distance starting from zero.
Let us find 2 × 6.
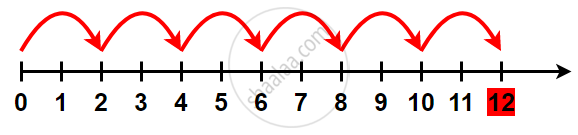
Start from 0, move 2 units at a time to the right, make such 6 moves.
You will reach 12. So, we say, 2 × 6 = 12.
4) Division on a number line:
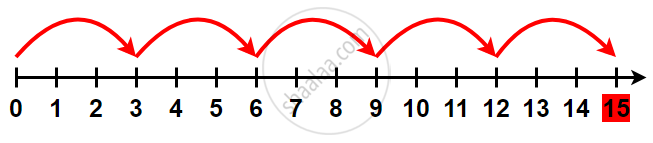
A number line can be used to divide. To work out 15 ÷ 3, count how many 'jumps' of 3 it takes to get from 0 to 15. 5 'jumps' or 'groups' of 5 means 15 ÷ 3 = 5.

