English
CISCEISC (Science) ISC Class 11
Question Papers17
Concept Notes & Videos164
Syllabus

Streamline and Turbulent Flow

Advertisements

Topics

  • Streamline flow
  • Laminar flow
  • Turbulent flow

Notes

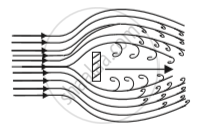
STREAMLINE FLOW:

The flow of a fluid is said to be steady if, at any point, the velocity of each passing fluid particle remains constant within that interval of time.

  • Streamline is the path followed by the fluid particle.

  • It means that at any particular instant the velocities of all the particles at any point are the same. But the velocity of all the particles won’t be the same across all the points in the space.

  • Steady flow is termed as ‘Streamline flow’ and ‘Laminar flow’.

Consider a case when all the particles of fluid passing point A have the same velocity. This means that the first particle will have velocity V1 and second will have velocity V1 and so on. All the particles will have the same velocity V1at point A.

At point B, all particles will have velocity V2.

Similarly, at point C the velocity of all the particles is V3.

We can see that the velocity is changing from point to point but at one particular point, it is the same.

  • No two streamlines can intersect.

  • If two streamlines intersect each other, the particles won’t know which path to follow and what velocity to attain. That is why no two streamlines intersect.

Equation of Continuity

  • According to the equation of continuity Av = constant. Where A =cross-sectional area and v=velocity with which the fluid flows.

  • It means that if any liquid is flowing in streamline flow in a pipe of non-uniform cross-section area, then the rate of flow of liquid across any cross-section remains constant.

  • Consider a fluid flowing through a tube of varying thickness.

Let the cross-sectional area at one end (l) = A1 and cross-sectional area of other end (ll) = A2

The velocity and density of the fluid at one end (l) = `v_1`,`rho_1` respectively velocity and density of the fluid at other end (ll) = `v_2,rho_2`

Volume covered by the fluid in a small interval of time `Delta"t"`, across left cross-sectional area(l) `="A"_1"xv"_1"x"Delta"t"`

 Volume covered by the fluid in a small interval of time `Delta"t"`, across left cross-sectional area(ll) `="A"_2"xv"_2"x"Delta"t"`

Fluid inside is incompressible (volume of fluid doesnot change by applying pressure) that is density remains same

`rho_1 = rho_2`         ...(1)

Along(l) mass = `rho_1A_1v_1Delta"t"` and along second point (ll) mass = `rho_2A_2v_2Delta"t"`

By eq (1), we can conclude that `"A"_1"v"_1="A"_2"v"_2`. This is the equation of continuity.

From Equation of continuity, we can say that Av=constant.
This equation is also termed as “Conservation of mass of incompressible fluids”.

Conclusion:

  1. The volume flux/Flow rate remains constant throughout the pipe. This means the rate of flow of fluid of liquidis is more if the cross-sectional area is more, then the velocity will be less, and vice-versa.

  2. But the Av will remain constant.

  3. So the volume which is covered by the fluid at any cross-sectional area is constant throughout the pipe even if the pipe has different cross-sectional areas.

  4. The fluid is accelerated while passing from the wider cross-sectional area towards the narrower area. This means if the area is more the velocity is less and vice-versa.

Problem:- The cylindrical tube of a spray pump has a cross-section of 8.0cm2 one end of which has 40 fine holes each of diameter 1.0mm. if the liquid flow inside the tube is 1.5m min-1, what is the speed of the ejection of the liquid through the holes?

Answer: 
Area of cross-section of the spray pump, `"A"_1`= 8cm2 = 8 x 10-4m2

number of holes, n=40

Diameter of each hole, d = 1mm = 1 x 10-3m

Radius of each hole, r = d/2 = 0.5 x 10-3m

Area of cross section of each hole, `a=pir^2 = pi(0.5xx10^-3)^2m^2`

Total area of 40 holes, `"A"_2=nxxa=40xxpi(0.5xx10^-3)^2m^2`

`=31.41 xx 10^-6m^2`

speed of flow of liquid inside the tube , `"V"_1=1.5  m//min = 0.025  m//s`

speed of ejection of liquid through the holes = `"V"_2`

According to the law of continuity we have:

`"A"_1"V"_1="A"_2"V"_2`

`"V"_2=("A"_1"V"_1)/"A"_2`

`=(8xx10^-4xx0.025) 31.61xx10^-6`

`=0.633  m//s`

 

Turbulent Flow:

  • Fluid flow is said to be turbulent if the velocity of the particles varies at any point erratically.

  • This means fluid particles are moving here and there, they are not moving in an organised manner. They all will have different velocities.

  • Eddies are generated by this flow. Eddies are the same as ripples.

  • All the particles are moving here and there randomly.

If you would like to contribute notes or other learning material, please submit them using the button below.

Related QuestionsVIEW ALL [10]

Along a streamline ______.

Water flows through two identical tubes A and B. A volume V0 of water passes through the tube A and 2 V0 through B in a given time. Which of the following may be correct?
(a) Flow in both the tubes are steady.
(b) Flow in both the tubes are turbulent.
(c) Flow is steady in A but turbulent in B.
(d) Flow is steady in B but turbulent in A.

Explain why When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers

Which of the following diagrams (Figure) does not represent a streamline flow?

Fill in the blanks using the word(s) from the list appended with each statement:

For a fluid in a steady flow, the increase in flow speed at a constriction follows (conservation of mass / Bernoulli’s principle)

Along a streamline, 

Streamline flow is more likely for liquids with ______.

Streamline flow is more likely for liquids with ______.

  1. high density.
  2. high viscosity.
  3. low density.
  4. low viscosity.
Advertisements
Share
Notifications

Englishहिंदीमराठी
Login
Create free account


      Forgot password?
Course
Use app×