Topics
Physical World and Measurement
Physical World
Units and Measurements
- International System of Units
- Measurement of Length
- Measurement of Mass
- Measurement of Time
- Accuracy, Precision and Least Count of Measuring Instruments
- Errors in Measurements
- Significant Figures
- Dimensions of Physical Quantities
- Dimensional Formulae and Dimensional Equations
- Dimensional Analysis and Its Applications
- Need for Measurement
- Units of Measurement
- Fundamental and Derived Units
- Length, Mass and Time Measurements
- Introduction of Units and Measurements
Motion in a Straight Line
- Position, Path Length and Displacement
- Average Velocity and Average Speed
- Instantaneous Velocity and Speed
- Kinematic Equations for Uniformly Accelerated Motion
- Acceleration (Average and Instantaneous)
- Relative Velocity
- Elementary Concept of Differentiation and Integration for Describing Motion
- Uniform and Non-uniform Motion
- Uniformly Accelerated Motion
- Position-time, Velocity-time and Acceleration-time Graphs
- Position - Time Graph
- Relations for Uniformly Accelerated Motion (Graphical Treatment)
- Introduction of Motion in One Dimension
- Motion in a Straight Line
Kinematics
Motion in a Plane
- Scalars and Vectors
- Multiplication of Vectors by a Real Number or Scalar
- Addition and Subtraction of Vectors - Graphical Method
- Resolution of Vectors
- Vector Addition – Analytical Method
- Motion in a Plane
- Motion in a Plane with Constant Acceleration
- Projectile Motion
- Uniform Circular Motion (UCM)
- General Vectors and Their Notations
- Motion in a Plane - Average Velocity and Instantaneous Velocity
- Rectangular Components
- Scalar (Dot) and Vector (Cross) Product of Vectors
- Relative Velocity in Two Dimensions
- Cases of Uniform Velocity
- Cases of Uniform Acceleration Projectile Motion
- Motion in a Plane - Average Acceleration and Instantaneous Acceleration
- Angular Velocity
- Introduction of Motion in One Dimension
Laws of Motion
Work, Energy and Power
Laws of Motion
- Aristotle’s Fallacy
- The Law of Inertia
- Newton's First Law of Motion
- Newton’s Second Law of Motion
- Newton's Third Law of Motion
- Conservation of Momentum
- Equilibrium of a Particle
- Common Forces in Mechanics
- Circular Motion and Its Characteristics
- Solving Problems in Mechanics
- Static and Kinetic Friction
- Laws of Friction
- Inertia
- Intuitive Concept of Force
- Dynamics of Uniform Circular Motion - Centripetal Force
- Examples of Circular Motion (Vehicle on a Level Circular Road, Vehicle on a Banked Road)
- Lubrication - (Laws of Motion)
- Law of Conservation of Linear Momentum and Its Applications
- Rolling Friction
- Introduction of Motion in One Dimension
Work, Energy and Power
- Introduction of Work, Energy and Power
- Notions of Work and Kinetic Energy: the Work-energy Theorem
- Kinetic Energy (K)
- Work Done by a Constant Force and a Variable Force
- Concept of Work
- Potential Energy (U)
- Conservation of Mechanical Energy
- Potential Energy of a Spring
- Various Forms of Energy : the Law of Conservation of Energy
- Power
- Collisions
- Non - Conservative Forces - Motion in a Vertical Circle
Motion of System of Particles and Rigid Body
System of Particles and Rotational Motion
- Motion - Rigid Body
- Centre of Mass
- Motion of Centre of Mass
- Linear Momentum of a System of Particles
- Vector Product of Two Vectors
- Angular Velocity and Its Relation with Linear Velocity
- Torque and Angular Momentum
- Equilibrium of Rigid Body
- Moment of Inertia
- Theorems of Perpendicular and Parallel Axes
- Kinematics of Rotational Motion About a Fixed Axis
- Dynamics of Rotational Motion About a Fixed Axis
- Angular Momentum in Case of Rotation About a Fixed Axis
- Rolling Motion
- Momentum Conservation and Centre of Mass Motion
- Centre of Mass of a Rigid Body
- Centre of Mass of a Uniform Rod
- Rigid Body Rotation
- Equations of Rotational Motion
- Comparison of Linear and Rotational Motions
- Values of Moments of Inertia for Simple Geometrical Objects (No Derivation)
Gravitation
Gravitation
- Kepler’s Laws
- Newton’s Universal Law of Gravitation
- The Gravitational Constant
- Acceleration Due to Gravity of the Earth
- Acceleration Due to Gravity Below and Above the Earth's Surface
- Acceleration Due to Gravity and Its Variation with Altitude and Depth
- Gravitational Potential Energy
- Escape Speed
- Earth Satellites
- Energy of an Orbiting Satellite
- Geostationary and Polar Satellites
- Weightlessness
- Escape Velocity
- Orbital Velocity of a Satellite
Properties of Bulk Matter
Mechanical Properties of Solids
- Elastic Behaviour of Solid
- Stress and Strain
- Hooke’s Law
- Stress-strain Curve
- Young’s Modulus
- Determination of Young’s Modulus of the Material of a Wire
- Shear Modulus or Modulus of Rigidity
- Bulk Modulus
- Application of Elastic Behaviour of Materials
- Elastic Energy
- Poisson’s Ratio
Thermodynamics
Behaviour of Perfect Gases and Kinetic Theory of Gases
Mechanical Properties of Fluids
- Thrust and Pressure
- Pascal’s Law
- Variation of Pressure with Depth
- Atmospheric Pressure and Gauge Pressure
- Hydraulic Machines
- Streamline and Turbulent Flow
- Applications of Bernoulli’s Equation
- Viscous Force or Viscosity
- Reynold's Number
- Surface Tension
- Effect of Gravity on Fluid Pressure
- Terminal Velocity
- Critical Velocity
- Excess of Pressure Across a Curved Surface
- Introduction of Mechanical Properties of Fluids
- Archimedes' Principle
- Stoke's Law
- Equation of Continuity
- Torricelli's Law
Oscillations and Waves
Thermal Properties of Matter
- Heat and Temperature
- Measurement of Temperature
- Ideal-gas Equation and Absolute Temperature
- Thermal Expansion
- Specific Heat Capacity
- Calorimetry
- Change of State - Latent Heat Capacity
- Conduction
- Convection
- Radiation
- Newton’s Law of Cooling
- Qualitative Ideas of Black Body Radiation
- Wien's Displacement Law
- Stefan's Law
- Anomalous Expansion of Water
- Liquids and Gases
- Thermal Expansion of Solids
- Green House Effect
Thermodynamics
- Thermal Equilibrium
- Zeroth Law of Thermodynamics
- Heat, Internal Energy and Work
- First Law of Thermodynamics
- Specific Heat Capacity
- Thermodynamic State Variables and Equation of State
- Thermodynamic Process
- Heat Engine
- Refrigerators and Heat Pumps
- Second Law of Thermodynamics
- Reversible and Irreversible Processes
- Carnot Engine
Kinetic Theory
- Molecular Nature of Matter
- Gases and Its Characteristics
- Equation of State of a Perfect Gas
- Work Done in Compressing a Gas
- Introduction of Kinetic Theory of an Ideal Gas
- Interpretation of Temperature in Kinetic Theory
- Law of Equipartition of Energy
- Specific Heat Capacities - Gases
- Mean Free Path
- Kinetic Theory of Gases - Concept of Pressure
- Assumptions of Kinetic Theory of Gases
- RMS Speed of Gas Molecules
- Degrees of Freedom
- Avogadro's Number
Oscillations
- Periodic and Oscillatory Motion
- Simple Harmonic Motion (S.H.M.)
- Simple Harmonic Motion and Uniform Circular Motion
- Velocity and Acceleration in Simple Harmonic Motion
- Force Law for Simple Harmonic Motion
- Energy in Simple Harmonic Motion
- Some Systems Executing Simple Harmonic Motion
- Damped Simple Harmonic Motion
- Forced Oscillations and Resonance
- Displacement as a Function of Time
- Periodic Functions
- Oscillations - Frequency
- Simple Pendulum
Waves
- Reflection of Transverse and Longitudinal Waves
- Displacement Relation for a Progressive Wave
- The Speed of a Travelling Wave
- Principle of Superposition of Waves
- Introduction of Reflection of Waves
- Standing Waves and Normal Modes
- Beats
- Doppler Effect
- Wave Motion
- Speed of Wave Motion
- Multiplication of a vector by a real number
- Multiplication of a vector by a scalar
Notes
Multiplication of Vectors by real numbers
Multiplying a vector A with a positive number λ gives a vector whose magnitude is changed by the factor λ but the direction is the same as that of A: |λA| = λ|A| if λ > 0
For example, if A is multiplied by 2, the resultant vector 2A is in the same direction as A and has a magnitude twice of |A| as shown in Fig. (a) below.
Multiplying a vector A by a negative number −λ gives another vector whose direction is opposite to the direction of A and whose magnitude is λ times |A|.
Multiplying a given vector A by negative numbers, say –1 and –1.5, gives vectors as shown in Fig (b) below. The factor λ by which a vector A is multiplied could be a scalar having its own physical dimension. Then, the dimension of λ A is the product of the dimensions of λ and A. For example, if we multiply a constant velocity vector by duration (of time), we get a displacement vector.
The factor λ by which a vector A is multiplied could be a scalar having its own physical dimension. Then, the dimension of λ A is the product of the dimensions of λ and A. For example, if we multiply a constant velocity vector by duration (of time), we get a displacement vector.
Dot product or scalar product:-
The dot product of two vectors A and B, is a scalar, which is equal to the product of the magnitudes of A and B and the Cosine of the smaller angle between them. If Θ is the smaller angle between A and B, then AB = AB
`bar A.bar B=ABcosθ`
(i) `hat i.hat i=hat j. hat j=hat k.hat k=1`
(ii) `hat i.hat j=hat j.hat k=hat k.hat i=0`
(iii) If `barA=A_x hat i +A_y hat j +A_z hat k and barB=B_x hat i +B_y hat j +B_z hat k`
then `barA .bar B=A_x B_x +A_y B_x +A_z B_z`
Properties of Scalar product:-
1. It obeys commutative law.
`barA .bar B=barB .bar A`
2. It obeys distributive law.
`barA .(bar B + bar C)= barA .bar B+ barA .bar C`
3. Scalar (Dot) product of two mutually perpendicular vectors is zero i.e.
`(barA .bar B) = AB cos 90^o=0`
4. Scalar (Dot) product will be maximum when θ = 0o i.e., vectors are parallel to each other.
`(barA .bar B)_(max)= |A||B|`
5. If `bar a ` and `bar b` are unit vectors then `|bar a|=|bar b|=1`and `bar a.bar b=1.1 cos θ= cos θ`
6. Dot product of unit vectors `hat i, hat j, hat k`
`hat i. hat i =hat j. hat j =hat k. hat k = 1
hat i. hat j =hat j. hat k =hat k. hat i = 0`
7. Square of a vector `bar a . bar a =|a||a| cos 0=a^2`
8. If the two vectors `bar A` and `bar B`, in terms of their rectangular components, are `barA=A_x hat i +A_y hat j +A_z hat k and barB=B_x hat i +B_y hat j +B_z hat k`
then `barA .bar B=(A_x hat i +A_y hat j +A_z hat k)(B_x hat i +B_y hat j +B_z hat k)`
`barA .bar B=A_x B_x +A_y B_x +A_z B_z`
Vector product(Cross product):
The cross product of two vectors and, represented by x is a vector, which is equal to the product of the magnitudes of A and B and the sine of the smaller angle between them. If Θ is the smaller angle between A and B, then = AB Sin θ
where `hat n` is a unit vector perpendicular to the plane containing `bar A` and `bar B`.
(i) `hat i × hat i =hat j × hat j =hat k × hat k = 0`
(ii) `hat i × hat j =hat k, hat j × hat k =hat i, hat k × hat i =hat j`
`hat j × hat i =`-`hat k`, `hat k × hat j =`-`hat i, hat i × hat k =`-`hat j`
(iii) If `barA=A_x hat i +A_y hat j +A_z hat k and barB=B_x hat i +B_y hat j +B_z hat k`
`bar A × bar B = (A_x B_z- A_z B_y) hat i +(A_z B_x- A_x B_z) hat j +(A_x B_y- A_y B_x) hat k `
Properties of Cross Product
(i) Cross product of two vectors is not commutative
`bar a × bar b ≠ bar b × bar a`
`bar a × bar b =-bar b × bar a`
(ii) Cross product is not assosiative
`bar a × (bar b × bar c) ≠ (bar a × bar b) × bar c`
(iii) Cross product obeys distributive law
`bar a × (bar b + bar c) = bar a × bar b + bar a × bar c`
(iv) If θ = 0 or `pi` it means the two vectors are collinear.
`bar a × bar b = bar 0`
and conversely, if `bar a × bar b = bar 0` then the vector `bar a` and `bar b` are parallel provided `bar a` and `bar b` are non-zero vectors.
(v) If θ = 90o, and `hat n` is the unit vector perpendicular to both `bar a` and `bar b`
`bar a × bar b=|a||b| sin 90^o hat n =|a||b| hat n`
(vi) The vector product of any vector with itself is `bar 0`
`bar a × bar a = bar 0`
(vii) If `bar a × bar b = bar 0`,then
`bar a=0 or bar b =0 or bar a|| bar b`
(viii) If `bar a ` and `bar b` are unit vectors, then `bar a × bar b=1.1 sin θ hat n = sin θ hat n`
(ix) Cross product of unit vectors `hat i, hat j and hat k`
`hat i × hat i =hat j × hat j =hat k × hat k = 0`
`hat i × hat j =hat k = - hat j × hat j`
`hat j × hat k =hat i = -hat k × hat j`
`hat k × hat i =hat j = -hat i × hat k`
(x) If the two vectors `bar A` and `bar B` in terms of their rectangular components are
`bar A = a_1 hat i + b_1 hat j + c_1 hat k`
`bar B = a_2 hat i + b_2 hat j + c_2 hat k`
`bar A × bar B = (a_1 hat i + b_1 hat j + c_1 hat k)×( a_2 hat i + b_2 hat j + c_2 hat k`)
It can be found by the determinant method
i.e., `bar A × bar B =[(hat i,hat j,hat k),("a"_1 ,"b"_1,"c"_1),("a"_2,"b"_2,"c"_2)]`
`= hat i(b_1 c_2 - b_2 c_1) - hat j(a_1 c_2 - a_2 c_1) + hat k(a_1 b_2 - a_2 b_1) `
- For motion in a plane, velocity is defined as:
`bar v =(bar r_2 - bar r_1)/(t_2 - t_1)= ((x_2 hat i + y_2 hat j) - (x_1 hat i + y_1 hat j))/((t_2 - t_1)) = (x_2 - x_1)/(t_2 - t_1) hat i + (y_2 - y_1)/(t_2 - t_1) hat j = v_x hat i and v = sqrt(a_x^2 + a_y^2) ` - For motion in a plane, acceleration is defined as:
`bar a =(bar v_2 - bar v_1)/(t_2 - t_1)= ((v_(x_2) hat i + v_(y_2) hat j) - (v_(x_1) hat i + v_(y_1) hat j))/((t_2 - t_1)) = ((v_(x_2) - v_(x_1))/(t_2 - t_1)) hat i + ((v_(y_2) - v_(y_1))/(t_2 - t_1)) hat j and v = sqrt(a_x^2 + a_y^2) `
Notes
Multiplication of Vectors by real numbers
Multiplying a vector A with a positive number λ gives a vector whose magnitude is changed by the factor λ but the direction is the same as that of A: |λA| = λ|A|, if λ > 0
For example, if A is multiplied by 2, the resultant vector 2A is in the same direction as A and has a magnitude twice of |A| as shown in Fig. (a) below.
Multiplying a vector A by a negative number −λ gives another vector whose direction is opposite to the direction of A and whose magnitude is λ times |A|.
Multiplying a given vector A by negative numbers, say –1 and –1.5, gives vectors as shown in Fig (b) below.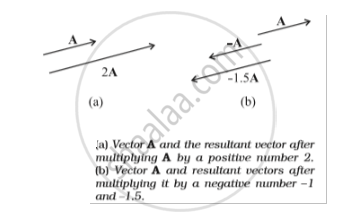
The factor λ by which a vector A is multiplied could be a scalar having its own physical dimension. Then, the dimension of λ A is the product of the dimensions of λ and A. For example, if we multiply a constant velocity vector by duration (of time), we get a displacement vector.
Related QuestionsVIEW ALL [3]
If |A| = 2 and |B| = 4, then match the relations in column I with the angle θ between A and B in column II
| Column I | Column II |
| (a) |A × B| = 0 | (i) θ = 30° |
| (b) |A × B| = 8 | (ii) θ = 45° |
| (c) |A × B| = 4 | (iii) θ = 90° |
| (d) |A × B| = `4sqrt(2)` | (iv) θ = 0° |