Advertisements
Advertisements
प्रश्न
एक दूसरे से 45° पर झुकी हुई दो सड़कों के संधि-स्थल से दो मनुष्य A तथा B, एक ही समय v वेग से चलना प्रारम्भ करते हैं। यदि वे अलग-अलग सड़कों पर चलते हैं तो उनके परस्पर एक दूसरे से अलग होने की दर ज्ञात कीजिए।
Advertisements
उत्तर
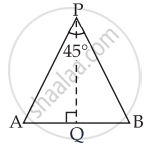
मान लीजिए P कोई ऐसा बिंदु है जिस पर दोनों सड़कें 45° के कोण पर झुकी हुई हैं।
दो आदमी A और B समान गति ‘V’ के साथ क्रमशः PA और PB सड़कों पर चल रहे हैं
माना A और B उनकी अंतिम स्थिति इस प्रकार है कि AB = y
∠APB = 45° और वे समान चाल से चलते हैं।
∴ ΔAPB एक समद्विबाहु त्रिभुज है।
PQ ⊥ AB खींचिए
AB = y
∴ AQ = `y/2` तथा PA = PB = x ...(माना)
∠APQ = ∠BPQ
= `45/2`
= `22 1/2^circ`
[∵ एक समद्विबाहु Δ में, शीर्ष से खींची गई ऊंचाई, आधार को समद्विभाजित करती है]
अब दायीं ओर ΔAPQ में,
`sin 22 1/2^circ = "AQ"/"AP"`
⇒ `sin 22 1/2^circ = 2/x = y/(2x)`
⇒ y = `2x * sin 22 1/2^circ`
दोनों पक्षों को w.r.t, t, से अलग करने पर, हम प्राप्त करते हैं
`"dy"/"dt" = 2 * "dx"/"dt" * sin 22 1/2^circ`
= `2 * "V" * sqrt(2 - sqrt(2))/2` ......`["क्योंकि" sin 22 1/2^circ = sqrt(2 - sqrt(2))/2]`
= `sqrt(2 - sqrt(2))` V m/s
इसलिए, उनके अलग होने की दर `sqrt(2 - sqrt(2))` V unit/s है।
APPEARS IN
संबंधित प्रश्न
वक्र y = 5x – 2x3 के लिए, यदि x में 2 इकाई/से. की दर से वृद्धि हो रही है, तो x = 3 पर वक्र का प्रावण्य कितनी तीव्रता से परिवर्तित हो रहा है?
सिद्ध कीजिए कि फलन f(x) = tanx – 4x अंतराल `((-pi)/3, pi/3)` निरंतर हासमान है।
निर्धारित कीजिए कि x के किन मानों के लिए, फलन y = `x^4 – (4x^3)/3` वर्धमान है तथा किन मानों के लिए, यह हासमान है।
सिद्ध कीजिए कि वक्र x = 3cos θ – cos3θ, y = 3sinθ – sin3θ के किसी बिंदु पर अभिंलब का समीकरण 4 (y cos3θ – x sin3θ) = 3 sin 4θ
उस महत्तम आयत का क्षेत्रफल ज्ञात कीजिए, जो दीर्घवृत्त `x^2/a^2 + y^2/b^2` = 1 के अंतर्गत स्थित है।
शीर्ष कोण `2theta` वाला एक समद्धिबाहु त्रिभुज a त्रिज्या वाले किसी वृत्त के अंतर्गत स्थित है। सिद्ध कीजिए कि त्रिभुजं का क्षेत्रफल उच्चतम है। जब `theta = pi/6`
वक्र y = sinx के बिंदु (0, 0) पर अभिलंब का समीकरण:
यदि f (x) = sinx तो अंतराल `[(-pi)/2, pi/2]` में f का निम्निष्ठ मान ______ है।
नमक का एक गोलाकार गेंद पानी में इस प्रकार घुल रहा है कि किसी क्षण उसके आयतन के घटने की दर उसके पृष्ठीय क्षेत्रफल के समानुपाती है। सिद्ध कीजिए कि उसकी त्रिज्या एक अचर दर से घट रही है।
एक पतंग 151.5 cm की ऊंचाई पर क्षैतिज दिशा में गतिमान है। यदि पतंग की चाल 10 m/s है, तो डोरी को कितनी तेजी से छोड़ा जा रहा है, जब उसकी दूरी पतंग उड़ाने वाले लड़के से 250 cm है? लड़के की ऊंचाई 1.5 m है।
2m लंबा एक मनुष्य 1`2/3` m/s की दर से किसी बिजली के खंभे की ओर, जो जमीन से 5`1/3`m ऊपर है, चल रहा है। उसकी छाया का अग्रभाग किसी दर से गतिमान है? उसकी छाया की लंबाई, उस समय किस दर से परिवर्तित हो रही है, जब वह प्रकाश के स्रोत के आधार से 3`1/3`m दूर है?
किसी तरनताल को सफाई के लिए खाली करना है।यदि ताल को बंद करने के t seconds बाद ताल में पानी की मात्रा, लिटर में, L से निरूपित होती है तथा L = 200 (10 – t)2 तो 5 seconds में अंत में पानी कितनी तेजी से बाहर निकल रहा है? प्रथम 5 seconds में पानी के बाहर निकलने की औसत दर क्या है?
सिद्ध किजिए कि f (x) = tan–1(sinx + cosx), अतंराल 0,`pi/4` में एक वर्धमान फलन है।
c2 क्षेत्रफल के किसी दिए हुए गत्ते से वर्गाकार आधार का एक खुला हुआ बाक्स बनाना है। सिद्ध कीजिए कि बाक्स का महत्तम आयतन `c^3/(6sqrt3)` घन इकाई है।
यदि किसी घन तथा गोले के पृष्ठीय क्षेत्रफल का योगफल अचर है तो घन के एक कोर (edge) तथा गोले के व्यास का अनुपात उस समय क्या है जब उनके आयतन का योगफल निम्नतम है?
AB किसी वृत्त का एक व्यास है तथा C उसकी परिधि पर कोई बिंदु है। सिद्ध कीजिए कि ∆ ABC का क्षेत्रफल महत्तम उस समय होगा जब वह समद्धिबाहु है।
किसी समबाहु त्रिभुज की भुजाएँ 2 cm/sec की दर से बढ़ रही हैं। जब भुजा 10 cm है, त्रिभुज का क्षेत्रफल ______ की दर से बढ़ता है।
निम्नलिखित में से कौन-सा फलन 0, `pi/2` में हासमान है,
यदि x एक वास्तविक संख्या है, तो x2 – 8x + 17 का निम्नतम मान ______
sin x . cos x का उच्चतम मान है ______
f(x) = xx का स्तब्ध बिंदु है ______
वक्र y = tanx के (0, 0) पर अभिलंब का समीकरण ______ है।
a के वे मान जिनके लिए फलन f (x) = sinx – ax + b, R में वर्धमान है ______ .हैं।
फलन f(x) = `"a"x + "b"/x` (a > 0, b > 0, x > 0) का निम्नतम मान ______ है।
