Advertisements
Advertisements
प्रश्न
Evaluate: `(5cos^2 60° + 4sec^2 30° - tan^2 45°)/(sin^2 30° + sin^2 60°)`
उत्तर
We will use the known values of trigonometric functions at specific angles:
cos 60° = `1/2`
sec 30° = `1/(cos 30°) = 2/sqrt3`
tan 45° = 1
Calculating the numerator:
`5cos^2 60° + 4sec^2 30° − tan^2 45°` = `5 (1/2)^2 + 4(2/sqrt3)^2 − 1^2`
= `5(1/4) + 4(4/3) − 1`
= `5/4 + 16/3 − 1`
Calculating the denominator:
`sin^2 30° + sin^2 60° = (1/2)^2 + (sqrt3/2)^2`
`= 1/4 + 3/4`
= 1
Therefore, the expression simplifies to:
`((5/4) + 16/3 - 1)/1`
= `5/4 + 16/3 - 1`
Converting the fractions to a common denominator and simplifying:
= `(15 + 64 - 12)/12`
= `67/12`
So, the evaluated result is `67/12`.
APPEARS IN
संबंधित प्रश्न
Evaluate: tan 7° tan 23° tan 60° tan 67° tan 83°
Evaluate: `(3 cos 55^@)/(7 sin 35^@) - (4(cos 70 cosec 20^@))/(7(tan 5^@ tan 25^@ tan 45^@ tan 65^@ tan 85^@))`
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: sin 45°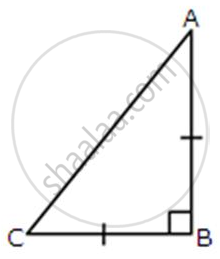
If A = B = 45° ,
show that:
cos (A + B) = cos A cos B - sin A sin B
Prove that : cos60° . cos30° - sin60° . sin30° = 0
Find the value of x in the following: 2 sin3x = `sqrt(3)`
If A = 30° and B = 60°, verify that: `(sin("A" + "B"))/(cos"A" . cos"B")` = tanA + tanB
If A = 30° and B = 60°, verify that: `(sin("A" -"B"))/(sin"A" . sin"B")` = cotB - cotA
Verify the following equalities:
cos 90° = 1 – 2sin2 45° = 2cos2 45° – 1
If sin α = `1/2`, then find the value of (3 cos α – 4 cos3 α).
