Advertisements
Advertisements
प्रश्न
Find the coordinates of the foot of the perpendicular from the point (−1, 3) to the line 3x − 4y − 16 = 0.
उत्तर
Let A (−1, 3) be the given point.
Also, let M (h, k) be the foot of the perpendicular drawn from A (−1, 3) to the line 3x − 4y − 16 = 0
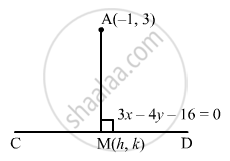
Point M (h, k) lies on the line 3x − 4y − 16 = 0
3h − 4k − 16 = 0 ... (1)
Lines 3x − 4y − 16 = 0 and AM are perpendicular.
\[\therefore\] \[\frac{k - 3}{h + 1} \times \frac{3}{4} = - 1\]
\[\Rightarrow 4h + 3k - 5 = 0\] ... (2)
Solving eq (1) and eq (2) by cross multiplication, we get:
\[\frac{h}{20 + 48} = \frac{k}{- 64 + 15} = \frac{1}{9 + 16}\]
\[ \Rightarrow a = \frac{68}{25}, b = - \frac{49}{25}\]
Hence, the coordinates of the foot of perpendicular are \[\left( \frac{68}{25}, - \frac{49}{25} \right)\].
APPEARS IN
संबंधित प्रश्न
Reduce the following equation into intercept form and find their intercepts on the axes.
3y + 2 = 0
Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.
Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2, find equation of the other line.
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes.
The hypotenuse of a right angled triangle has its ends at the points (1, 3) and (−4, 1). Find the equation of the legs (perpendicular sides) of the triangle that are parallel to the axes.
Find the equation of the line which intercepts a length 2 on the positive direction of the x-axis and is inclined at an angle of 135° with the positive direction of y-axis.
Find the equation of the right bisector of the line segment joining the points A (1, 0) and B (2, 3).
Find the equations of the sides of the triangles the coordinates of whose angular point is respectively (1, 4), (2, −3) and (−1, −2).
Find the equation of the bisector of angle A of the triangle whose vertices are A (4, 3), B (0, 0) and C(2, 3).
Point R (h, k) divides a line segment between the axes in the ratio 1 : 2. Find the equation of the line.
Find the equation of a line for p = 8, α = 300°.
Find the equation of the straight line on which the length of the perpendicular from the origin is 2 and the perpendicular makes an angle α with x-axis such that sin α = \[\frac{1}{3}\].
Find the equation of the straight line upon which the length of the perpendicular from the origin is 2 and the slope of this perpendicular is \[\frac{5}{12}\].
Find the equation of a straight line on which the perpendicular from the origin makes an angle of 30° with x-axis and which forms a triangle of area \[50/\sqrt{3}\] with the axes.
Reduce the following equation to the normal form and find p and α in \[x + \sqrt{3}y - 4 = 0\] .
Reduce the following equation to the normal form and find p and α in \[x - y + 2\sqrt{2} = 0\].
Reduce the following equation to the normal form and find p and α in x − 3 = 0.
Show that the origin is equidistant from the lines 4x + 3y + 10 = 0; 5x − 12y + 26 = 0 and 7x + 24y = 50.
Find the point of intersection of the following pairs of lines:
2x − y + 3 = 0 and x + y − 5 = 0
Find the coordinates of the vertices of a triangle, the equations of whose sides are x + y − 4 = 0, 2x − y + 3 = 0 and x − 3y + 2 = 0.
Prove that the following sets of three lines are concurrent:
3x − 5y − 11 = 0, 5x + 3y − 7 = 0 and x + 2y = 0
Find the equation of the straight line which has y-intercept equal to \[\frac{4}{3}\] and is perpendicular to 3x − 4y + 11 = 0.
Find the image of the point (2, 1) with respect to the line mirror x + y − 5 = 0.
Find the projection of the point (1, 0) on the line joining the points (−1, 2) and (5, 4).
Find the values of α so that the point P (α2, α) lies inside or on the triangle formed by the lines x − 5y+ 6 = 0, x − 3y + 2 = 0 and x − 2y − 3 = 0.
Find the values of the parameter a so that the point (a, 2) is an interior point of the triangle formed by the lines x + y − 4 = 0, 3x − 7y − 8 = 0 and 4x − y − 31 = 0.
Determine whether the point (−3, 2) lies inside or outside the triangle whose sides are given by the equations x + y − 4 = 0, 3x − 7y + 8 = 0, 4x − y − 31 = 0 .
Write the coordinates of the orthocentre of the triangle formed by the lines x2 − y2 = 0 and x + 6y = 18.
The point which divides the join of (1, 2) and (3, 4) externally in the ratio 1 : 1
The number of real values of λ for which the lines x − 2y + 3 = 0, λx + 3y + 1 = 0 and 4x − λy + 2 = 0 are concurrent is
Find the equation of a line which passes through the point (2, 3) and makes an angle of 30° with the positive direction of x-axis.
The inclination of the line x – y + 3 = 0 with the positive direction of x-axis is ______.
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is ______.
Reduce the following equation into slope-intercept form and find their slopes and the y-intercepts.
y = 0
Reduce the following equation into intercept form and find their intercepts on the axes.
3x + 2y – 12 = 0
Reduce the following equation into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
x − y = 4
