Advertisements
Advertisements
प्रश्न
Find the value of 'A', if cot 3A = 1
उत्तर
cot 3A = 1
⇒ cot 3A = cot 45°
⇒ 3A = 45°
⇒ A = 15°.
APPEARS IN
संबंधित प्रश्न
If 4 cos2 x° - 1 = 0 and 0 ∠ x° ∠ 90°,
find:(i) x°
(ii) sin2 x° + cos2 x°
(iii) `(1)/(cos^2xx°) – (tan^2 xx°)`
If sin 3A = 1 and 0 < A < 90°, find sin A
If 4 cos2 x = 3 and x is an acute angle;
find the value of :
(i) x
(ii) cos2 x + cot2 x
(iii) cos 3x (iv) sin 2x
Find the value 'x', if: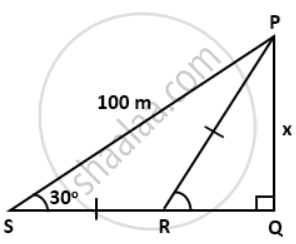
In the given figure, if tan θ = `(5)/(13), tan α = (3)/(5)` and RS = 12m, find the value of 'h'.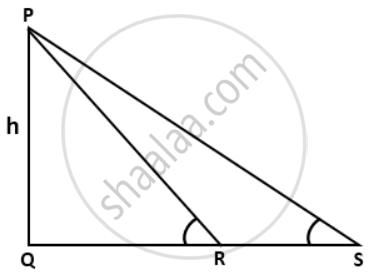
Evaluate the following: `(sin62°)/(cos28°)`
Evaluate the following: sin22° cos44° - sin46° cos68°
Express each of the following in terms of trigonometric ratios of angles between 0° and 45°: cos84° + cosec69° - cot68°
Evaluate the following: `(3sin37°)/(cos53°) - (5"cosec"39°)/(sec51°) + (4tan23° tan37° tan67° tan53°)/(cos17° cos67° "cosec"73° "cosec"23°)`
Prove the following: `(tan(90° - θ)cotθ)/("cosec"^2 θ)` = cos2θ
