Advertisements
Advertisements
प्रश्न
Find the value of 'A', if (1 - cosec A)(2 - sec A) = 0
उत्तर
(1 - cosec A)(2 - sec A) = 0
⇒ 1 - cosec A = 0 and 2 - sec A = 0
⇒ cosec A = 1 and sec A = 2
⇒ cosec A = cosec 90° and sec A = sec 60°
⇒ A = 90° and A = 60°.
APPEARS IN
संबंधित प्रश्न
Use the given figure to find:
(i) tan θ°
(ii) θ°
(iii) sin2θ° - cos2θ°
(iv) Use sin θ° to find the value of x.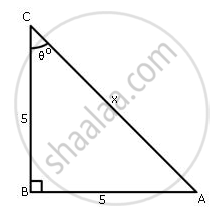
Solve for x : 2 cos 3x - 1 = 0
Calculate the value of A, if (sec 2A - 1) (cosec 3A - 1) = 0
Solve for x : cos2 30° + sin2 2x = 1
Solve for 'θ': `sec(θ/2 + 10°) = (2)/sqrt(3)`
Find x and y, in each of the following figure: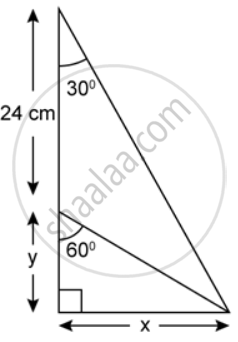
Evaluate the following: cot20° cot40° cot45° cot50° cot70°
Evaluate the following: `(sin0° sin35° sin55° sin75°)/(cos22° cos64° cos58° cos90°)`
If secθ= cosec30° and θ is an acute angle, find the value of 4 sin2θ - 2 cos2θ.
Prove the following: tanθ tan(90° - θ) = cotθ cot(90° - θ)
