Advertisements
Advertisements
प्रश्न
Form the differential equation of all circles which pass through origin and whose centres lie on y-axis.
उत्तर
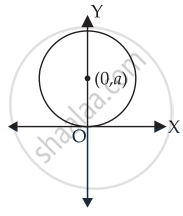
Equation of circle which passes through the origin and whose centre lies on y-axis is
(x – 0)2 + (y – a)2 = a2
⇒ x2 + y2 + a2 – 2ay = a2
⇒ x2 + y2 – 2ay = 0 ......(i)
Differentiating both sides w.r.t. x we get
⇒ `2x + 2y * "dy"/"dx" - 2"a" * "dy"/"dx"` = 0
⇒ `x + y "dy"/"dx" - "a" * "dy"/"dx"` = 0
⇒ `x + (y - "a") * "dy"/"dx"` = 0
`y - "a" = x/("dy"/"dx")`
a = `y + (-x)/("dy"/"dx")`
Putting the value of a in equation (i), we get
`x^2 + y^2 - 2(y + x/("dy"/"dx"))y` = 0
⇒ `x^2 + y^2 - 2y^2 - (2xy)/("dy"/"dx")` = 0
⇒ `x^2 - y^2 = (2xy)/("dy"/"dx")`
∴ `(x^2 - y^2) "dy"/"dx" - 2xy` = 0
Hence, the required differential equation is `(x^2 - y^2) "dy"/"dx" - 2xy` = 0
APPEARS IN
संबंधित प्रश्न
Form the differential equation of the family of circles touching the y-axis at the origin.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Which of the following differential equation has y = x as one of its particular solution?
A. `(d^2y)/(dx^2) - x^2 (dy)/(dx) + xy = x`
B. `(d^2y)/(dx^2) + x dy/dx + xy = x`
C. `(d^2y)/(dx^2) - x^2 dy/dx + xy = 0`
D. `(d^2y)/(dx^2) + x dy/dx + xy = 0`
Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.
Form the differential equation of the family of curves represented by y2 = (x − c)3.
Form the differential equation from the following primitive where constants are arbitrary:
y2 = 4ax
Form the differential equation from the following primitive where constants are arbitrary:
xy = a2
Form the differential equation of the family of curves represented by the equation (a being the parameter):
(2x − a)2 − y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
x2 + y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
y2 = 4ax
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
x2 + (y − b)2 = 1
Find the equation of a curve passing through the point (0, 0) and whose differential equation is \[\frac{dy}{dx} = e^x \sin x\]
Find one-parameter families of solution curves of the following differential equation:-
\[x\frac{dy}{dx} - y = \left( x + 1 \right) e^{- x}\]
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} - \frac{2xy}{1 + x^2} = x^2 + 2\]
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} \cos^2 x = \tan x - y\]
Find one-parameter families of solution curves of the following differential equation:-
\[e^{- y} \sec^2 y dy = dx + x dy\]
The differential equation which represents the family of curves y = eCx is
Form the differential equation representing the family of curves y = mx, where m is an arbitrary constant.
Form the differential equation representing the family of curves y = e2x (a + bx), where 'a' and 'b' are arbitrary constants.
Form the differential equation representing the family of curves y = A sin x, by eliminating the arbitrary constant A.
Find the differential equation of the family of curves y = Ae2x + B.e–2x.
The differential equation representing the family of curves y = A sinx + B cosx is ______.
The differential equation `y ("d"y)/("d"x) + "c"` represents: ______.
The differential equation representing the family of circles x2 + (y – a)2 = a2 will be of order two.
Differential equation representing the family of curves y = ex (Acosx + Bsinx) is `("d"^2y)/("d"x^2) - 2 ("d"y)/("d"x) + 2y` = 0
From the differential equation of the family of circles touching the y-axis at origin
