Advertisements
Advertisements
प्रश्न
If a function g = {(1, 1), (2, 3), (3, 5), (4, 7)} is described by g(x) = \[\alpha x + \beta\] then find the values of \[\alpha\] and \[ \beta\] . [NCERT EXEMPLAR]
उत्तर
We have,
A function g = {(1, 1), (2, 3), (3, 5), (4, 7)} is described by g(x) =
\[\alpha x + \beta\]
\[As, g\left( 1 \right) = 1 \text{ and g}\left( 2 \right) = 3\]
\[So, \alpha\left( 1 \right) + \beta = 1\]
\[ \Rightarrow \alpha + \beta = 1 . . . . . \left( i \right)\]
\[\text{ and } \alpha\left( 2 \right) + \beta = 3\]
\[ \Rightarrow 2\alpha + \beta = 3 . . . . . \left( ii \right)\]
\[\left( ii \right) - \left( i \right), \text{we get}\]
\[2\alpha - \alpha = 2\]
\[ \Rightarrow \alpha = 2\]
\[\text{Substituting} \alpha = 2 in \left( i \right), \text{ we get}\]
\[2 + \beta = 1\]
\[ \Rightarrow \beta = - 1\]
APPEARS IN
संबंधित प्रश्न
Let f: N → N be defined by f(n) = `{((n+1)/2, ",if n is odd"),(n/2,",n is even"):}` for all n ∈ N.
State whether the function f is bijective. Justify your answer.
Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but gis not injective.
(Hint: Consider f(x) = x and g(x) =|x|)
Give an example of a function which is neither one-one nor onto ?
Which of the following functions from A to B are one-one and onto?
f1 = {(1, 3), (2, 5), (3, 7)} ; A = {1, 2, 3}, B = {3, 5, 7}
Which of the following functions from A to B are one-one and onto ?
f3 = {(a, x), (b, x), (c, z), (d, z)} ; A = {a, b, c, d,}, B = {x, y, z}.
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = sinx
If A = {1, 2, 3}, show that a one-one function f : A → A must be onto.
Suppose f1 and f2 are non-zero one-one functions from R to R. Is `f_1 / f^2` necessarily one - one? Justify your answer. Here,`f_1/f_2 : R → R is given by (f_1/f_2) (x) = (f_1(x))/(f_2 (x)) for all x in R .`
Find gof and fog when f : R → R and g : R → R is defined by f(x) = 2x + 3 and g(x) = x2 + 5 .
Consider f : R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Let A = R - {3} and B = R - {1}. Consider the function f : A → B defined by f(x) = `(x-2)/(x-3).`Show that f is one-one and onto and hence find f-1.
[CBSE 2012, 2014]
If f : R → (0, 2) defined by `f (x) =(e^x - e^(x))/(e^x +e^(-x))+1`is invertible , find f-1.
If A = {1, 2, 3, 4} and B = {a, b, c, d}, define any four bijections from A to B. Also give their inverse functions.
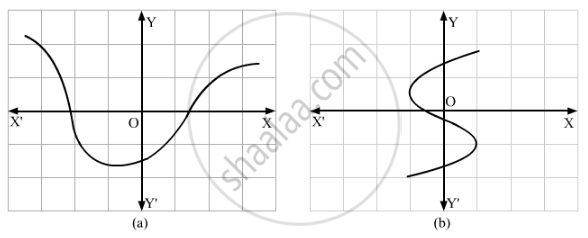
Which one of the following graphs represents a function?
Let \[f : \left[ - \frac{\pi}{2}, \frac{\pi}{2} \right] \to\] A be defined by f(x) = sin x. If f is a bijection, write set A.
What is the range of the function
`f (x) = ([x - 1])/(x -1) ?`
Let f : R → R be the function defined by f(x) = 4x − 3 for all x ∈ R Then write f . [NCERT EXEMPLAR]
Let A = {a, b, c, d} and f : A → A be given by f = {( a,b ),( b , d ),( c , a ) , ( d , c )} write `f^-1`. [NCERT EXEMPLAR]
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
The function f : [-1/2, 1/2, 1/2] → [-π /2,π/2], defined by f (x) = `sin^-1` (3x - `4x^3`), is
If A = {a, b, c, d} and f = {a, b), (b, d), (c, a), (d, c)}, show that f is one-one from A onto A. Find f–1
Let R be the set of real numbers and f: R → R be the function defined by f(x) = 4x + 5. Show that f is invertible and find f–1.
Let the function f: R → R be defined by f(x) = cosx, ∀ x ∈ R. Show that f is neither one-one nor onto
Let X = {1, 2, 3}and Y = {4, 5}. Find whether the following subset of X ×Y are function from X to Y or not
g = {(1, 4), (2, 4), (3, 4)}
Let A = R – {3}, B = R – {1}. Let f: A → B be defined by f(x) = `(x - 2)/(x - 3)` ∀ x ∈ A . Then show that f is bijective
Let f: `[2, oo)` → R be the function defined by f(x) = x2 – 4x + 5, then the range of f is ______.
If f(x) = (4 – (x – 7)3}, then f–1(x) = ______.
The function f : R → R defined by f(x) = 3 – 4x is ____________.
Which of the following functions from Z into Z is bijective?
Let f : R → R be a function defined by f(x) `= ("e"^abs"x" - "e"^-"x")/("e"^"x" + "e"^-"x")` then f(x) is
Let f : [0, ∞) → [0, 2] be defined by `"f" ("x") = (2"x")/(1 + "x"),` then f is ____________.
Let f : R → R, g : R → R be two functions such that f(x) = 2x – 3, g(x) = x3 + 5. The function (fog)-1 (x) is equal to ____________.
Consider a function f: `[0, pi/2] ->` R, given by f(x) = sinx and `g[0, pi/2] ->` R given by g(x) = cosx then f and g are
Let f: R→R be a polynomial function satisfying f(x + y) = f(x) + f(y) + 3xy(x + y) –1 ∀ x, y ∈ R and f'(0) = 1, then `lim_(x→∞)(f(2x))/(f(x)` is equal to ______.
Let f(x) be a polynomial of degree 3 such that f(k) = `-2/k` for k = 2, 3, 4, 5. Then the value of 52 – 10f(10) is equal to ______.
Let f(x) be a polynomial function of degree 6 such that `d/dx (f(x))` = (x – 1)3 (x – 3)2, then
Assertion (A): f(x) has a minimum at x = 1.
Reason (R): When `d/dx (f(x)) < 0, ∀ x ∈ (a - h, a)` and `d/dx (f(x)) > 0, ∀ x ∈ (a, a + h)`; where 'h' is an infinitesimally small positive quantity, then f(x) has a minimum at x = a, provided f(x) is continuous at x = a.
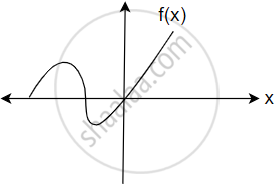
The given function f : R → R is not ‘onto’ function. Give reason.
