Advertisements
Advertisements
प्रश्न
If f(x) = (4 – (x – 7)3}, then f–1(x) = ______.
उत्तर
If f(x) = (4 – (x – 7)3}, then f–1(x) = `7 + (4 - x)^(1/3)`.
Explanation:
Given that, f(x) = [4 – (x – 7)3]
Let y = [4 – (x – 7)3]
⇒ (x – 7)3) = 4 – y
⇒ (x – 7) = `(4 - y)^(1/3)`
⇒ x = 7 + `(4 - y)^(1/3)`
⇒ f–1(x) = `7 + (4 - x)^(1/3)`
APPEARS IN
संबंधित प्रश्न
Let A and B be sets. Show that f: A × B → B × A such that (a, b) = (b, a) is bijective function.
Let S = {a, b, c} and T = {1, 2, 3}. Find F−1 of the following functions F from S to T, if it exists.
F = {(a, 2), (b, 1), (c, 1)}
Classify the following function as injection, surjection or bijection : f : N → N given by f(x) = x3
Classify the following function as injection, surjection or bijection :
f : Z → Z, defined by f(x) = x2 + x
Classify the following function as injection, surjection or bijection :
f : R → R, defined by f(x) = x3 − x
Set of ordered pair of a function ? If so, examine whether the mapping is injective or surjective :{(a, b) : a is a person, b is an ancestor of a}
Find fog (2) and gof (1) when : f : R → R ; f(x) = x2 + 8 and g : R → R; g(x) = 3x3 + 1.
Consider f : {1, 2, 3} → {a, b, c} and g : {a, b, c} → {apple, ball, cat} defined as f (1) = a, f (2) = b, f (3) = c, g (a) = apple, g (b) = ball and g (c) = cat. Show that f, g and gof are invertible. Find f−1, g−1 and gof−1and show that (gof)−1 = f −1o g−1
Consider the function f : R+ → [-9 , ∞ ]given by f(x) = 5x2 + 6x - 9. Prove that f is invertible with f -1 (y) = `(sqrt(54 + 5y) -3)/5` [CBSE 2015]
Let f : [−1, ∞) → [−1, ∞) be given by f(x) = (x + 1)2 − 1, x ≥ −1. Show that f is invertible. Also, find the set S = {x : f(x) = f−1 (x)}.
Let A and B be two sets, each with a finite number of elements. Assume that there is an injective map from A to B and that there is an injective map from B to A. Prove that there is a bijection from A to B.
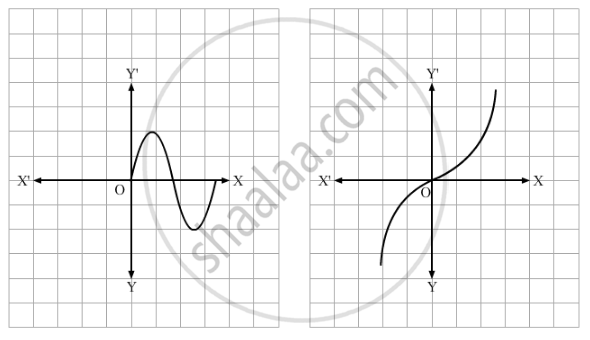
Which of the following graphs represents a one-one function?
If f : R → R is defined by f(x) = x2, find f−1 (−25).
\[f : A \to \text{B given by } 3^{ f\left( x \right)} + 2^{- x} = 4\] is a bijection, then
\[f : R \to R\] is defined by
\[f\left( x \right) = \frac{e^{x^2} - e^{- x^2}}{e^{x^2 + e^{- x^2}}} is\]
Let \[f\left(x\right) = x^3\] be a function with domain {0, 1, 2, 3}. Then domain of \[f^{-1}\] is ______.
Let A = R − (2) and B = R − (1). If f: A ⟶ B is a function defined by`"f(x)"=("x"-1)/("x"-2),` how that f is one-one and onto. Hence, find f−1.
Write about strlen() function.
Let f: R → R be defined by f(x) = x2 + 1. Then, pre-images of 17 and – 3, respectively, are ______.
The smallest integer function f(x) = [x] is ____________.
Sherlin and Danju are playing Ludo at home during Covid-19. While rolling the dice, Sherlin’s sister Raji observed and noted the possible outcomes of the throw every time belongs to set {1,2,3,4,5,6}. Let A be the set of players while B be the set of all possible outcomes.
A = {S, D}, B = {1,2,3,4,5,6}
- Raji wants to know the number of functions from A to B. How many number of functions are possible?
An organization conducted a bike race under 2 different categories-boys and girls. Totally there were 250 participants. Among all of them finally, three from Category 1 and two from Category 2 were selected for the final race. Ravi forms two sets B and G with these participants for his college project. Let B = {b1,b2,b3} G={g1,g2} where B represents the set of boys selected and G the set of girls who were selected for the final race.
Ravi decides to explore these sets for various types of relations and functions.
- Let R: B → G be defined by R = { (b1,g1), (b2,g2),(b3,g1)}, then R is ____________.
Let f: R → R defined by f(x) = 3x. Choose the correct answer
If f; R → R f(x) = 10x + 3 then f–1(x) is:
Consider a function f: `[0, pi/2] ->` R, given by f(x) = sinx and `g[0, pi/2] ->` R given by g(x) = cosx then f and g are
Consider a set containing function A= {cos–1cosx, sin(sin–1x), sinx((sinx)2 – 1), etan{x}, `e^(|cosx| + |sinx|)`, sin(tan(cosx)), sin(tanx)}. B, C, D, are subsets of A, such that B contains periodic functions, C contains even functions, D contains odd functions then the value of n(B ∩ C) + n(B ∩ D) is ______ where {.} denotes the fractional part of functions)
Find the domain of sin–1 (x2 – 4).
