Advertisements
Advertisements
प्रश्न
In any ΔABC, with usual notations, prove that b2 = c2 + a2 – 2ca cos B.
उत्तर
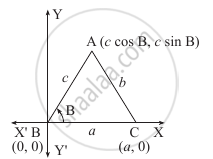
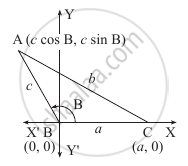
Let us take the angle B of ΔABC in standard position,
i.e. B as origin, X-axis along the line BC and the Y-axis perpendicular to the line BC.
In the two figures, ∠B is shown as acute in one and obtuse in the other.
∵ l(BC) = a
∴ C ≡ (a, 0)
Let A ≡ (x, y)
Since l (BA) = c, we have
cos B = `x/c` and sin B = `y/c`
∴ x = c cos B and y = c sin B
∴ A ≡ (c cos B, c sin B)
∴ By the distance formula
b2 = AC2 = (a – c cos B)2 + (0 – c sin B)2
= a2 – 2ca cos B + c2 cos2B + c2 sin2B
= c2(cos2B + sin2B) + a2 – 2ca cos B
∴ b2 = c2 + a2 – 2ca cos B.
APPEARS IN
संबंधित प्रश्न
In ΔABC, prove that `tan((A - B)/2) = (a - b)/(a + b)*cot C/2`
In ΔABC with usual notations, prove that 2a `{sin^2(C/2)+csin^2 (A/2)}` = (a + c - b)
In Δ ABC, if a = 13, b = 14 and c = 15, then sin (A/2)= _______.
(A) `1/5`
(B) `sqrt(1/5)`
(C) `4/5`
(D) `2/5`
If in ∆ABC with usual notations a = 18, b = 24, c = 30 then sin A/2 is equal to
(A) `1/sqrt5`
(B) `1/sqrt10`
(C) `1/sqrt15`
(D) `1/(2sqrt5)`
With usual notations, in ΔABC, prove that a(b cos C − c cos B) = b2 − c2
In , ΔABC prove that
`"sin"(("B" - "C")/2) = (("b" - "c")/"a") "cos"("A"/2)`
In ,Δ ABC with usual notations prove that
b2 = c2 +a2 - 2 ca cos B
Find the Cartesian co-ordinates of the point whose polar co-ordinates are:
`(sqrt(2), pi/4)`
Find the Cartesian coordinates of the point whose polar coordinates are :
`(4, pi/2)`
Find the Cartesian co-ordinates of the point whose polar co-ordinates are:
`(3/4, (3pi)/4)`
Find the Cartesian co-ordinates of the point whose polar co-ordinates are:
`(1/2, (7pi)/3)`
Find the polar co-ordinates of the point whose Cartesian co-ordinates are.
`(0, 1/2)`
Find the polar co-ordinates of the point whose Cartesian co-ordinates are.
`(3/2, (3√3)/2)`.
In any Δ ABC, prove the following:
`("b" - "c")/"a" = (tan "B"/2 - tan "C"/2)/(tan "B"/2 +tan "C"/2)`
In Δ ABC, if ∠C = 90°, then prove that sin (A - B) = `("a"^2 - "b"^2)/("a"^2 + "b"^2)`
In ΔABC, if `"cos A"/"a" = "cos B"/"b"`, then show that it is an isosceles triangle.
In Δ ABC, if sin2 A + sin2 B = sin2 C, then show that the triangle is a right-angled triangle.
With the usual notations, show that
(c2 − a2 + b2) tan A = (a2 − b2 + c2) tan B = (b2 − c2 + a2) tan C
Show that
`tan^-1(1/5) + tan^-1(1/7) + tan^-1(1/3) + tan^-1 (1/8) = pi/4.`
Show that `(9pi)/8 - 9/4 sin^-1 (1/3) = 9/4 sin^-1 ((2sqrt2)/3)`.
If sin `(sin^-1 1/5 + cos^-1 x) = 1`, then find the value of x.
If `tan^-1 (("x" - 1)/("x" - 2)) + tan^-1 (("x" + 1)/("x" + 2)) = pi/4`, find the value of x.
State whether the following equation has a solution or not?
cos 2θ = `1/3`
Solve: `tan^-1 ("1 - x"/"1 + x") = 1/2 (tan^-1 "x")`, for x > 0.
In ∆ABC, if cos A = `(sinB)/(2sinC)`, then ∆ABC is ______.
In ΔABC, a = 3, b = 4 and sin A = `3/4`, find ∠B
With usual notations, prove that `(cos "A")/"a" + (cos "B")/"b" + (cos "C")/"c" = ("a"^2 + "b"^2 + "c"^2)/(2"abc")`
In ∆ABC, prove that `("b" - "c")^2 cos^2 ("A"/2) + ("b" + "c")^2 sin^2 ("A"/2)` = a2
In ΔABC, if a cos A = b cos B, then prove that ΔABC is either a right angled or an isosceles triangle.
In ∆ABC, prove that `(cos 2"A")/"a"^2 - (cos 2"c")/"c"^2 = 1/"a"^2 - 1/"c"^2`
In ∆ABC, if `(2cos "A")/"a" + (cos "B")/"b" + (2cos"C")/"c" = "a"/"bc" + "b"/"ca"`, then show that the triangle is a right angled
In ∆ABC, prove that `sin ((A - B)/2) = ((a - b)/c) cos C/2`
In ∆ABC, prove that `(cos^2"A" - cos^2"B")/("a" + "b") + (cos^2"B" - cos^2"C")/("b" + "c") + (cos^2"C" - cos^2"A")/("c" + "a")` = 0
In ΔABC, prove that `("a"^2sin("B" - "C"))/(sin"A") + ("b"^2sin("C" - "A"))/(sin"B") + ("c"^2sin("A" - "B"))/(sin"C")` = 0
In ΔABC, prove that `("b"^2 - "c"^2)/"a" cos"A" + ("c"^2 - "a"^2)/"b" cos"B" + ("a"^2 - "b"^2)/"c" cos "C"` = 0
In ∆ABC, if ∠A = `pi/2`, then prove that sin(B − C) = `("b"^2 - "c"^2)/("b"^2 + "c"^2)`
In ΔABC, if (a+ b - c)(a + b + c) = 3ab, then ______.
In a ΔABC, cot `(("A - B")/2)* tan (("A + B")/2)` is equal to
In a ΔABC if 2 cos C = sin B · cosec A, then ______.
In a triangle ABC with usual notations, if `(cos "A")/"a" = (cos "B")/"b" = (cos "C")/"c"`, then area of triangle ABC with a = `sqrt6` is ____________.
If in a right-angled triangle ABC, the hypotenuse AB = p, then `overline"AB".overline" AC" + overline"BC".overline" BA" + overline" CA".overline"CB"` is equal to ______
In Δ ABC; with usual notations, if cos A = `(sin "B")/(sin "C")`, then the triangle is _______.
In a ΔABC, `(sin "C"/2)/(cos(("A" - "B")/2))` = ______
If one side of a triangle is double the other and the angles opposite to these sides differ by 60°, then the triangle is ______
In Δ ABC; with usual notations, `("b" sin "B" - "c" sin "C")/(sin ("B - C"))` = _______.
In Δ ABC, with the usual notations, if `(tan "A"/2)(tan "B"/2) = 3/4` then a + b = ______.
In ΔABC if sin2A + sin2B = sin2C and l(AB) = 10, then the maximum value of the area of ΔABC is ______
If cartesian co-ordinates of a point are `(1, -sqrt3)`, then its polar co-ordinates are ______
If polar co-ordinates of a point are `(1/2, pi/2)`, then its cartesian co-ordinates are ______.
If in Δ ABC, 3a = b + c, then `cot ("B"/2) cot ("C"/2)` = ______.
In `triangleABC,` if a = 3, b = 4, c = 5, then sin 2B = ______.
If in a `triangle"ABC",` a2cos2 A - b2 - c2 = 0, then ______.
If in ΔABC, `sin "B"/2 sin "C"/2 = sin "A"/2` and 2s is the perimeter of the triangle, then s is ______.
In ΔABC, if `"a" cos^2 "C"/2 + "c" cos^2 "A"/2 = (3"b")/2`, then a, b, c are in ______.
In ΔABC, `cos"A"/"a" = cos"B"/"b" cos"C"/"c"`. If a = `1/sqrt(6)`, then the area of the triangle is ______.
If a = 13, b = 14, c = 15, then `cos("A"/2)` = ______.
In a ΔABC, if a = `sqrt(2)` x and b = 2y and ∠C = 135°, then the area of triangle is ______.
Find the cartesian co-ordinates of the point whose polar co-ordinates are `(1/2, π/3)`.
If in a triangle ABC, AB = 5 units, AB = 5 units, ∠B = `cos^-1 (3/5)` and radius of circumcircle of ΔABC is 5 units, then the area (in sq.units) of ΔABC is ______.
In a triangle ABC, ∠C = 90°, then `(a^2 - b^2)/(a^2 + b^2)` is ______.
In any ΔABC, prove that:
(b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c.
The perimeter of ΔABC is 20, ∠A = 60°, area of ΔABC = `10sqrt(3)`, then find the values of a, b, c.
In ΔABC, a = 3, b = 1, cos(A – B) = `2/9`, find c.
