Advertisements
Advertisements
प्रश्न
किसी बास्केट बॉल टीम द्वारा मैचों की एक श्रृंखला में निम्नलिखित प्वाइंट अर्जित किए गए :
17, 2, 7, 27, 25, 5, 14, 18, 10, 24, 48, 10, 8, 7, 10, 28
इन आँकड़ों के लिए माध्यक और बहुलक ज्ञात कीजिए।
उत्तर
आँकड़ों पर विचार करें -
17, 2, 7, 27, 25, 5, 14, 18, 10, 24, 48, 10, 8, 7, 10, 28
दिए गए अंकों को आरोही क्रम में व्यवस्थित करें, हमें मिलता है -
2, 5, 7, 7, 8, 10, 10, 14, 17, 18, 24, 25, 27, 28, 48
इस आँकड़ों में दिए गए प्रेक्षणों की संख्या 16 है जो कि सम है।
तो, माध्यिका की गणना निम्नानुसार की जाएगी -
माध्यिका = `((n/2)^("वाँ") "प्रेक्षण" + (n/2 + 1)^("वाँ") "प्रेक्षण")/2`
= `((16/2)^("वाँ") "प्रेक्षण" + (16/2 + 1)^("वाँ") "प्रेक्षण")/2`
= `((8)^("वाँ") "प्रेक्षण" + (9)^("वाँ") "प्रेक्षण")/2`
= `(10 + 14)/2`
= `24/2`
= 12
जैसा कि हम जानते हैं कि, बहुलक वह प्रेक्षण है जिसे अधिकतम 10 बार दोहराया जाता है।
अत:, दिए गए आंकड़ों के लिए माध्यिका और बहुलक क्रमशः 12 और 10 हैं।
APPEARS IN
संबंधित प्रश्न
निम्न सारणी से एक फैक्टरी में काम कर रहे 60 कर्मचारियों का माध्य वेतन मान ज्ञात कीजिए।
| वेतन (रुपये में) | श्रमिकों की संख्या |
| 3000 | 16 |
| 4000 | 12 |
| 5000 | 10 |
| 6000 | 8 |
| 7000 | 6 |
| 8000 | 4 |
| 9000 | 3 |
| 10000 | 1 |
| कुल | 60 |
पाँच संख्याओं का माध्य 30 है। यदि इनमें से एक संख्या को हटा दिया जाए, तो उनका माध्य 28 हो जाता है। हटाई गई संख्या है
यदि x1, x2, ..., xn का माध्य `barx` है, तो a ≠ 0, के लिए `ax_1, ax_2, ..., ax_n, x_1/a, x_2/a, ..., x_n/a` का माध्य है
100 प्रेक्षणों का माध्य 50 है। यदि इनमें से एक प्रेक्षण 50 को 150 से प्रतिस्थापित कर दिया जाए तो परिणामी माध्य हो जाएगा :
50 संख्याएँ दी हुई हैं। इनमें से प्रत्येक संख्या को 53 में से घटाया जाता है तथा इस प्रकार प्राप्त संख्याओं का माध्य –3.5 ज्ञात किया जाता है। दी हुई संख्याओं का माध्य है :
एक संग्रह में से 80 बल्ब यादृच्छिक रूप से चुने जाते हैं और उनके जीवन कालों (घंटों में) को निम्नलिखित बारंबारता सारणी के रूप में रिकार्ड किया गया :
| जीवन काल (घंटों में) | 300 | 500 | 700 | 900 | 1100 |
| बारंबारता | 10 | 12 | 23 | 25 | 10 |
इस संग्रह में से एक बल्ब यादृच्छिक रूप से चुना जाता है। इस बल्ब का जीवन काल 1150 घंटा होने की प्रायिकता है :
निम्नलिखित आँकड़ों से एक सतत बारंबारता बंटन तैयार कीजिए :
| मध्य-बिंदु | बारंबारता |
| 5 | 4 |
| 15 | 8 |
| 25 | 13 |
| 35 | 12 |
| 45 | 6 |
वर्ग अंतरालों के माप भी ज्ञात कीजिए।
यदि निम्नलिखित आँकड़ों का माध्य 20.2 है, तो p का मान ज्ञात कीजिए :
| x | 10 | 15 | 20 | 25 | 30 |
| f | 6 | 8 | p | 10 | 6 |
निम्नलिखित बंटन का माध्य ज्ञात कीजिए :
| बारंबारताएँ | चर |
| 4 | 4 |
| 8 | 6 |
| 14 | 8 |
| 11 | 10 |
| 3 | 12 |
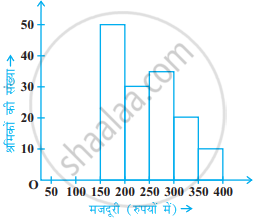
निम्नलिखित आकृति में, एक आयतचित्र दिया है जो किसी फैक्ट्री की श्रमिकों की दैनिक मजदूरी दर्शाता है। इसके लिए एक बारंबारता बंटन सारणी की रचना कीजिए।