Advertisements
Advertisements
प्रश्न
Prove the following:
If tan A = `3/4`, then sinA cosA = `12/25`
उत्तर
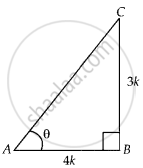
Given, tan A = `3/4 = "P"/"B" = "Perpendicular"/"Base"`
Let P = 3k and B = 4k
By Pythagoras theorem,
H2 = P2 + B2
= (3k)2 + (4k)2
= 9k2 + 16k2
= 25k2
⇒ H = 5k ...[Since, side cannot be negative]
∴ sin A = `"P"/"H" = (3"k")/(5"k") = 3/5`
And cos A = `"B"/"H" = (4"k")/(5"k") = 4/5`
Now, sin A cos A = `3/5 * 4/5 = 12/25`
Hence proved.
APPEARS IN
संबंधित प्रश्न
State whether the following are true or false. Justify your answer.
sec A = `12/5` for some value of angle A.
Prove that `(sin "A" - 2sin^3 "A")/(2cos^3 "A" - cos "A") = tan "A"`
In the following, trigonometric ratios are given. Find the values of the other trigonometric ratios.
`sin theta = 11/5`
If 3 tan θ = 4, find the value of `(4cos theta - sin theta)/(2cos theta + sin theta)`
Evaluate the following
`sin^2 30° cos^2 45 ° + 4 tan^2 30° + 1/2 sin^2 90° − 2 cos^2 90° + 1/24 cos^2 0°`
Find the value of x in the following :
`2 sin x/2 = 1`
If sin 2A = `1/2` tan² 45° where A is an acute angle, then the value of A is ______.
If A and (2A – 45°) are acute angles such that sin A = cos (2A – 45°), then tan A is equal to ______.
If cos A = `4/5`, then the value of tan A is ______.
If θ is an acute angle and sin θ = cos θ, find the value of tan2 θ + cot2 θ – 2.
