Advertisements
Advertisements
प्रश्न
The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number.
उत्तर
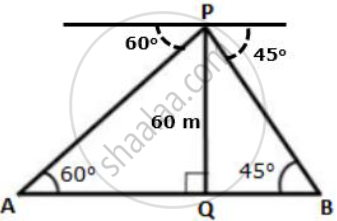
Let PQ be the light house.
`=>` PQ = 60
`tan 60^@ = (PQ)/(AQ)`
`=> sqrt(3) = 60/(AQ)`
`=> AQ = 60/sqrt(3)`
`=> AQ = (20 xx 3)/sqrt(3)`
`=> AQ = (20 xx sqrt(3) xx sqrt(3))/sqrt(3)`
`=> AQ = 20sqrt(3) m`
In ΔPQB
`tan 45^@ = (PQ)/(QB)`
`=> 1 = 60/(QB)`
`=>` QB = 60 m
Now,
AB = AQ + QB
= `20sqrt(3) + 60`
= 20 × 1.732 + 60
= 94.64
= 95 m
APPEARS IN
संबंधित प्रश्न
Prove the following trigonometric identities.
`(sec A - tan A)/(sec A + tan A) = (cos^2 A)/(1 + sin A)^2`
Prove the following identities:
`cosA/(1 - sinA) = sec A + tan A`
Prove the following identities:
`(sinA + cosA)/(sinA - cosA) + (sinA - cosA)/(sinA + cosA) = 2/(2sin^2A - 1)`
Prove the following identities:
cosec4 A (1 – cos4 A) – 2 cot2 A = 1
If a cot θ + b cosec θ = p and b cot θ − a cosec θ = q, then p2 − q2
Prove that `(tan^2"A")/(tan^2 "A"-1) + (cosec^2"A")/(sec^2"A"-cosec^2"A") = (1)/(1-2 co^2 "A")`
Prove that : `1 - (cos^2 θ)/(1 + sin θ) = sin θ`.
Prove the following identities.
tan4 θ + tan2 θ = sec4 θ – sec2 θ
Prove the following identities.
`costheta/(1 + sintheta)` = sec θ – tan θ
`5/(sin^2theta) - 5cot^2theta`, complete the activity given below.
Activity:
`5/(sin^2theta) - 5cot^2theta`
= `square (1/(sin^2theta) - cot^2theta)`
= `5(square - cot^2theta) ......[1/(sin^2theta) = square]`
= 5(1)
= `square`
