Advertisements
Advertisements
प्रश्न
The value of cos1°. cos2°. cos3°. cos4°....................... cos90° is ______.
विकल्प
1
0
–1
2
उत्तर
The value of cos1°. cos2°. cos3°. cos4°....................... cos90° is 0.
APPEARS IN
संबंधित प्रश्न
If x = 30°, verify that
(i) `\tan 2x=\frac{2\tan x}{1-\tan ^{2}x`
(ii) `\sin x=\sqrt{\frac{1-\cos 2x}{2}}`
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
cos 78° + sec 78°
Evaluate: `4(sin^2 30 + cos^4 60^@) - 2/3 3[(sqrt(3/2))^2 . [1/sqrt2]^2] + 1/4 (sqrt3)^2`
Evaluate: Cosec (65 + θ) – sec (25 – θ) – tan (55 – θ) + cot (35 + θ)
Prove that
cosec (67° + θ) − sec (23° − θ) = 0
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: sin 45°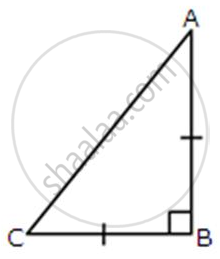
Without using tables, evaluate the following: sin230° cos245° + 4tan230° + sin290° + cos20°
Without using tables, find the value of the following: `(sin30°)/(sin45°) + (tan45°)/(sec60°) - (sin60°)/(cot45°) - (cos30°)/(sin90°)`
If A = 30° and B = 60°, verify that: `(sin("A" -"B"))/(sin"A" . sin"B")` = cotB - cotA
Verify cos3A = 4cos3A – 3cosA, when A = 30°
