Advertisements
Advertisements
प्रश्न
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used:
λ1 = 3650 Å, λ2 = 4047 Å, λ3 = 4358 Å, λ4 = 5461 Å, λ5 = 6907 Å,
The stopping voltages, respectively, were measured to be:
V01 = 1.28 V, V02 = 0.95 V, V03 = 0.74 V, V04 = 0.16 V, V05 = 0 V
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 × 10−19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
उत्तर
Einstein’s photoelectric equation is given as:
eV0 = hv − `phi_0`
`"V"_0 = "h"/"e" "v" - phi_0/"e"` .............(1)
Where,
V0 = Stopping potential
h = Planck’s constant
e = Charge on an electron
v = Frequency of radiation
`phi_0` = Work function of a material
It can be concluded from equation (1) that potential V0 is directly proportional to frequency v.
Frequency is also given by the relation:
`"v" = "Speed of light (c)"/"Wavelenght (λ)"`
This relation can be used to obtain the frequencies of the various lines of the given wavelengths.
`"v"_1 = "c"/lambda_1 = (3 xx 10^8)/(3650 xx 10^(-10)) = 8.219 xx 10^14 "Hz"`
`"v"_2 = "c"/lambda_2 = (3 xx10^8)/(4047 xx 10^(-10)) = 7.412 xx 10^14 "Hz"`
`"v"_3 = "c"/lambda_3 = (3 xx 10^8)/(4358 xx 10^(-10)) = 6.884 xx 10^14 "Hz"`
`"v"_4 = "c"/lambda_4 = (3 xx 10^8)/(5461 xx 10^(-10)) = 5.493 xx 10^14 "Hz"`
`"v"_5 = "c"/lambda_5 = (3xx10^8)/(6907 xx 10^(-10)) = 4.343 xx 10^14 "Hz"`
The given quantities can be listed in tabular form as:
| Frequency × 1014 Hz | 8.219 | 7.412 | 6.884 | 5.493 | 4.343 |
| Stopping potential V0 | 1.28 | 0.95 | 0.74 | 0.16 | 0 |
The following figure shows a graph between νand V0.
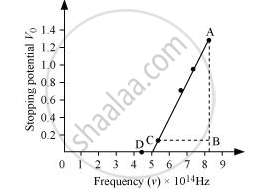
It can be observed that the obtained curve is a straight line. It intersects the ν-axis at 5 × 1014 Hz, which is the threshold frequency (v0) of the material. Point D corresponds to a frequency less than the threshold frequency. Hence, there is no photoelectric emission for the λ5 line, and therefore, no stopping voltage is required to stop the current.
Slope of the straight line = `"AB"/"CB" = (1.28 - 0.16)/((8.214 - 5.493) xx 10^14)`
From equation (1), the slope `"h"/"e"` can be written as:
`"h"/"e" = (1.28 - 0.16)/((8.214 - 5.493) xx 10^14)`
∴ `"h" = (1.12 xx 1.6 xx 10^(-19))/(2.726 xx 10^(14))`
= 6.573 × 10−34 Js
The work function of the metal is given as:
`phi_0` = hv0
= 6.573 × 10−34 × 5 × 1014
= 3.286 × 10−19 J
= `(3.286 xx 10^(-19))/(1.6 xx 1^(-18))`
= 2.054 eV
APPEARS IN
संबंधित प्रश्न
Light of intensity 10−5 W m−2 falls on a sodium photo-cell of surface area 2 cm2. Assuming that the top 5 layers of sodium absorb the incident energy, estimate time required for photoelectric emission in the wave-picture of radiation. The work function for the metal is given to be about 2 eV. What is the implication of your answer?
The following graph shows the variation of photocurrent for a photosensitive metal :
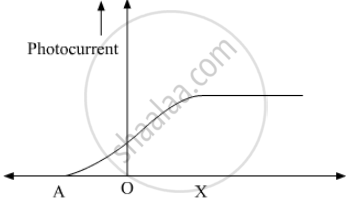
(a) Identify the variable X on the horizontal axis.
(b) What does the point A on the horizontal axis represent?
(c) Draw this graph for three different values of frequencies of incident radiation v1, v2 and v3 (v1 > v2 > v3) for same intensity.
(d) Draw this graph for three different values of intensities of incident radiation I1, I2 and I3 (I1 > I2 > I3) having same frequency.
Should the energy of a photon be called its kinetic energy or its internal energy?
When stopping potential is applied in an experiment on photoelectric effect, no photoelectric is observed. This means that
A point source of light is used in a photoelectric effect. If the source is removed farther from the emitting metal, the stopping potential
A point source causes photoelectric effect from a small metal plate. Which of the following curves may represent the saturation photocurrent as a function of the distance between the source and the metal?

When the intensity of a light source in increased,
(a) the number of photons emitted by the source in unit time increases
(b) the total energy of the photons emitted per unit time increases
(c) more energetic photons are emitted
(d) faster photons are emitted
If the wavelength of light in an experiment on photoelectric effect is doubled,
(a) photoelectric emission will not take place
(b) photoelectric emission may or may not take place
(c) the stopping potential will increase
(d) the stopping potential will decrease
Calculate the momentum of a photon of light of wavelength 500 nm.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Calculate the number of photons emitted per second by a 10 W sodium vapour lamp. Assume that 60% of the consumed energy is converted into light. Wavelength of sodium light = 590 nm
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A parallel beam of monochromatic light of wavelength 663 nm is incident on a totally reflecting plane mirror. The angle of incidence is 60° and the number of photons striking the mirror per second is 1.0 × 1019. Calculate the force exerted by the light beam on the mirror.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A totally reflecting, small plane mirror placed horizontally faces a parallel beam of light, as shown in the figure. The mass of the mirror is 20 g. Assume that there is no absorption in the lens and that 30% of the light emitted by the source goes through the lens. Find the power of the source needed to support the weight of the mirror.
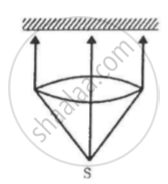
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
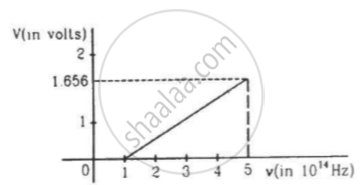
The figure is the plot of stopping potential versus the frequency of the light used in an experiment on photoelectric effect. Find (a) the ratio h/e and (b) the work function.
Define the term: stopping potential in the photoelectric effect.
In photoelectric effect the photo current ______.
Two monochromatic beams A and B of equal intensity I, hit a screen. The number of photons hitting the screen by beam A is twice that by beam B. Then what inference can you make about their frequencies?
Consider a thin target (10–2 cm square, 10–3 m thickness) of sodium, which produces a photocurrent of 100 µA when a light of intensity 100W/m2 (λ = 660 nm) falls on it. Find the probability that a photoelectron is produced when a photons strikes a sodium atom. [Take density of Na = 0.97 kg/m3].
If photons of ultraviolet light of energy 12 eV are incident on a metal surface of work function of 4 eV, then the stopping potential (in eV) will be :
Read the following paragraph and answer the questions.
| The figure shows the variation of photoelectric current measured in a photocell circuit as a function of the potential difference between the plates of the photocell when light beams A, B, C and D of different wavelengths are incident on the photocell. Examine the given figure and answer the following questions: |
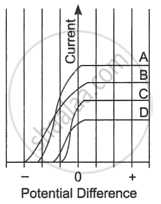
- Which light beam has the highest frequency and why?
- Which light beam has the longest wavelength and why?
- Which light beam ejects photoelectrons with maximum momentum and why?
