Advertisements
Advertisements
प्रश्न
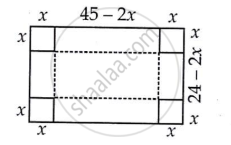
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
उत्तर
Let the side of the required square be x,
Length of the box (l) = (45 - 2x)
And width of the box (b) = (24 - 2x)
Height of the box (h) = x
∴ Volume of the box, V = l × b × h
V = x (45 - 2x) · (24 - 2x)
= (4x3 - 138x2 + 1080x) ...(1)
On differentiating equation (1) with respect to x,
`(dV)/dx =` 12x2 - 276x + 1080 ...(2)
For maximum value of V, `(dV)/dx = 0`
or 12x2 - 276x + 1080 = 0 or x2 - 23x + 90 = 0
or x2 - 18x - 5x + 90 = 0 or x(x - 18) - 5 (x - 18) = 0
or (x - 18)(x - 5) = 0
`therefore` x = 5, 18
Differentiating equation (2) again with respect to x, `(d^2V)/dx^2` = 24x - 276
At, x = 5 `(d^2V)/dx^2` = 24 × 5 - 276 = (negative value)
∴ The value of V will be maximum at x = 5.
∴ The side of the square will be 5 cm.
APPEARS IN
संबंधित प्रश्न
Find the approximate value of cos (89°, 30'). [Given is: 1° = 0.0175°C]
Find the maximum value of 2x3 − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Find two numbers whose sum is 24 and whose product is as large as possible.
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is `tan^(-1) sqrt(2)`
A rod of 108 meters long is bent to form a rectangle. Find its dimensions if the area is maximum. Let x be the length and y be the breadth of the rectangle.
Divide the number 20 into two parts such that sum of their squares is minimum.
Solve the following : Show that a closed right circular cylinder of given surface area has maximum volume if its height equals the diameter of its base.
Solve the following:
Find the maximum and minimum values of the function f(x) = cos2x + sinx.
A wire of length 120 cm is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum
A metal wire of 36 cm long is bent to form a rectangle. By completing the following activity, find it’s dimensions when it’s area is maximum.
Solution: Let the dimensions of the rectangle be x cm and y cm.
∴ 2x + 2y = 36
Let f(x) be the area of rectangle in terms of x, then
f(x) = `square`
∴ f'(x) = `square`
∴ f''(x) = `square`
For extreme value, f'(x) = 0, we get
x = `square`
∴ f''`(square)` = – 2 < 0
∴ Area is maximum when x = `square`, y = `square`
∴ Dimensions of rectangle are `square`
By completing the following activity, examine the function f(x) = x3 – 9x2 + 24x for maxima and minima
Solution: f(x) = x3 – 9x2 + 24x
∴ f'(x) = `square`
∴ f''(x) = `square`
For extreme values, f'(x) = 0, we get
x = `square` or `square`
∴ f''`(square)` = – 6 < 0
∴ f(x) is maximum at x = 2.
∴ Maximum value = `square`
∴ f''`(square)` = 6 > 0
∴ f(x) is maximum at x = 4.
∴ Minimum value = `square`
The maximum volume of a right circular cylinder if the sum of its radius and height is 6 m is ______.
The minimum value of Z = 5x + 8y subject to x + y ≥ 5, 0 ≤ x ≤ 4, y ≥ 2, x ≥ 0, y ≥ 0 is ____________.
If f(x) = 3x3 - 9x2 - 27x + 15, then the maximum value of f(x) is _______.
If R is the circum radius of Δ ABC, then A(Δ ABC) = ______.
The function y = 1 + sin x is maximum, when x = ______
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
If the sum of the surface areas of cube and a sphere is constant, what is the ratio of an edge of the cube to the diameter of the sphere, when the sum of their volumes is minimum?
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5/cm2 and the material for the sides costs Rs 2.50/cm2. Find the least cost of the box.
The smallest value of the polynomial x3 – 18x2 + 96x in [0, 9] is ______.
The curves y = 4x2 + 2x – 8 and y = x3 – x + 13 touch each other at the point ______.
Find the points of local maxima and local minima respectively for the function f(x) = sin 2x - x, where `-pi/2 le "x" le pi/2`
The function f(x) = x5 - 5x4 + 5x3 - 1 has ____________.
Find the volume of the largest cylinder that can be inscribed in a sphere of radius r cm.
A function f(x) is maximum at x = a when f'(a) > 0.
Let f: R → R be a function defined by f(x) = (x – 3)n1(x – 5)n2, n1, n2 ∈ N. Then, which of the following is NOT true?
If p(x) be a polynomial of degree three that has a local maximum value 8 at x = 1 and a local minimum value 4 at x = 2; then p(0) is equal to ______.
If the point (1, 3) serves as the point of inflection of the curve y = ax3 + bx2 then the value of 'a ' and 'b' are ______.
The sum of all the local minimum values of the twice differentiable function f : R `rightarrow` R defined by
f(x) = `x^3 - 3x^2 - (3f^('')(2))/2 x + f^('')(1)`
The minimum value of 2sinx + 2cosx is ______.
A rectangle with one side lying along the x-axis is to be inscribed in the closed region of the xy plane bounded by the lines y = 0, y = 3x and y = 30 – 2x. The largest area of such a rectangle is ______.
The minimum value of the function f(x) = xlogx is ______.
The maximum value of f(x) = `logx/x (x ≠ 0, x ≠ 1)` is ______.
A rod AB of length 16 cm. rests between the wall AD and a smooth peg, 1 cm from the wall and makes an angle θ with the horizontal. The value of θ for which the height of G, the midpoint of the rod above the peg is minimum, is ______.
Check whether the function f : R `rightarrow` R defined by f(x) = x3 + x, has any critical point/s or not ? If yes, then find the point/s.
If Mr. Rane order x chairs at the price p = (2x2 - 12x - 192) per chair. How many chairs should he order so that the cost of deal is minimum?
Solution: Let Mr. Rane order x chairs.
Then the total price of x chairs = p·x = (2x2 - 12x- 192)x
= 2x3 - 12x2 - 192x
Let f(x) = 2x3 - 12x2 - 192x
∴ f'(x) = `square` and f''(x) = `square`
f'(x ) = 0 gives x = `square` and f''(8) = `square` > 0
∴ f is minimum when x = 8
Hence, Mr. Rane should order 8 chairs for minimum cost of deal.
