Advertisements
Advertisements
प्रश्न
A system releases 130 kJ of heat while 109 kJ of work is done on the system. Calculate the change in internal energy.
उत्तर
Data: Q = −130 kJ, W = −109 kJ
Find: ΔU = ?
Calculations:
ΔU = Q − W
ΔU = −130 − (−109)
ΔU = −130 + 109
ΔU = −21 kJ
∴ The change in internal energy is −21 kJ. This is the change (decrease) in the internal energy.
संबंधित प्रश्न
Explain why Two bodies at different temperatures T1 and T2, if brought in thermal contact, do not necessarily settle to the mean temperature (T1 + T2)/2.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P-V-T surface?
A steam engine delivers 5.4×108 J of work per minute and services 3.6 × 109 J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
A cylinder containing a gas is lifted from the first floor to the second floor. What is the amount of work done on the gas? What is the amount of work done by the gas? Is the internal energy of the gas increased? Is the temperature of the gas increased?
When we rub our hands they become warm. Have we supplied heat to the hands?
A closed bottle contains some liquid. the bottle is shaken vigorously for 5 minutes. It is found that the temperature of the liquid is increased. Is heat transferred to the liquid? Is work done on the liquid? Neglect expansion on heating.
When a tyre bursts, the air coming out is cooler than the surrounding air. Explain.
Consider the following two statements.
(A) If heat is added to a system, its temperature must increase.
(B) If positive work is done by a system in a thermodynamic process, its volume must increase.
An ideal gas goes from the state i to the state f as shown in figure. The work done by the gas during the process ______________ .
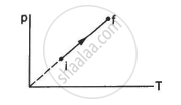
Consider two processes on a system as shown in figure.
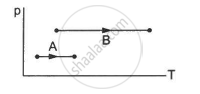
The volumes in the initial states are the same in the two processes and the volumes in the final states are also the same. Let ∆W1 and ∆W2 be the work done by the system in the processes A and B respectively.
The pressure p and volume V of an ideal gas both increase in a process.
(a) Such a process is not possible.
(b) The work done by the system is positive.
(c) The temperature of the system must increase.
(d) Heat supplied to the gas is equal to the change in internal energy.
In a process on a system, the initial pressure and volume are equal to the final pressure and volume.
(a) The initial temperature must be equal to the final temperature.
(b) The initial internal energy must be equal to the final internal energy.
(c) The net heat given to the system in the process must be zero.
(d) The net work done by the system in the process must be zero.
Figure shows three paths through which a gas can be taken from the state A to the state B. Calculate the work done by the gas in each of the three paths.
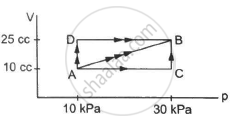
A substance is taken through the process abc as shown in figure. If the internal energy of the substance increases by 5000 J and a heat of 2625 cal is given to the system, calculate the value of J.
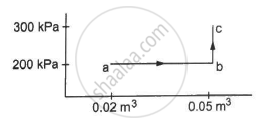
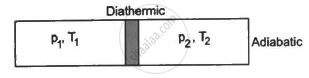
Figure shows a cylindrical tube of volume V with adiabatic walls containing an ideal gas. The internal energy of this ideal gas is given by 1.5 nRT. The tube is divided into two equal parts by a fixed diathermic wall. Initially, the pressure and the temperature are p1, T1 on the left and p2, T2 on the right. The system is left for sufficient time so that the temperature becomes equal on the two sides. (a) How much work has been done by the gas on the left part? (b) Find the final pressures on the two sides. (c) Find the final equilibrium temperature. (d) How much heat has flown from the gas on the right to the gas on the left?
Which of the following system freely allows the exchange of energy and matter with its environment?
What is the energy associated with the random, disordered motion of the molecules of a system called as?
Explain given cases related to energy transfer between the system and surrounding –
- energy transferred (Q) > 0
- energy transferred (Q) < 0
- energy transferred (Q) = 0
Explain the different ways through which the internal energy of the system can be changed.
One gram of water (1 cm3) becomes 1671 cm3 of steam at a pressure of 1 atm. The latent heat of vaporization at this pressure is 2256 J/g. Calculate the external work and the increase in internal energy.
In a thermodynamic system, working substance is ideal gas. Its internal energy is in the form of ______.
When 1 g of water at 0° C and 1 x 105 N/m2 pressure is converted into ice of volume 1.082 cm3, the external work done will be ____________.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
What is the change in internal energy of the gas?
n mole of a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes:
A `→` B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2 = 2V1 and pressure changes from P1 to P2.
B `→` C: Isobaric compression at pressure P2 to initial volume V1.
C `→` A: Isochoric change leading to change of pressure from P2 to P1.
Total workdone in the complete cycle ABCA is ______.

If a gas is compressed adiabatically:
Explain the change in internal energy of a thermodynamic system (the gas) by heating it.
