Advertisements
Advertisements
प्रश्न
An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be at least 4 successes.
उत्तर
The probability of success is twice the probability of failure.
Let the probability of failure be x.
∴ Probability of success = 2x
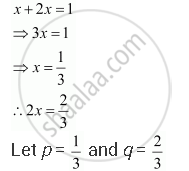
Let X be the random variable that represents the number of successes in six trials.
By binomial distribution, we obtain
P (X = x) = `""^nC_x P^(n-x) q^x`
Probability of at least 4 successes = P (X ≥ 4)
= P (X = 4) + P (X = 5) + P (X = 6)

APPEARS IN
संबंधित प्रश्न
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. What is the probability that out of 5 such bulbs
(i) none
(ii) not more than one
(iii) more than one
(iv) at least one, will fuse after 150 days of use.
In an examination, 20 questions of true-false type are asked. Suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads, he answers ‘true’; if it falls tails, he answers ‘false’. Find the probability that he answers at least 12 questions correctly.
The probability that a student is not a swimmer is 1/5 . Then the probability that out of five students, four are swimmers is
(A) `""^5C_4 (4/5)^4 1/5`
(B) `(4/5)^4 1/5
(C) `""^5C_1 1/5 (4/5)^4 `
(D) None of these
A bag contains 10 balls, each marked with one of the digits from 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
A bag contains 7 green, 4 white and 5 red balls. If four balls are drawn one by one with replacement, what is the probability that one is red?
A man wins a rupee for head and loses a rupee for tail when a coin is tossed. Suppose that he tosses once and quits if he wins but tries once more if he loses on the first toss. Find the probability distribution of the number of rupees the man wins.
Five dice are thrown simultaneously. If the occurrence of 3, 4 or 5 in a single die is considered a success, find the probability of at least 3 successes.
A card is drawn and replaced in an ordinary pack of 52 cards. How many times must a card be drawn so that (i) there is at least an even chance of drawing a heart (ii) the probability of drawing a heart is greater than 3/4?
The mathematics department has 8 graduate assistants who are assigned to the same office. Each assistant is just as likely to study at home as in office. How many desks must there be in the office so that each assistant has a desk at least 90% of the time?
Suppose that a radio tube inserted into a certain type of set has probability 0.2 of functioning more than 500 hours. If we test 4 tubes at random what is the probability that exactly three of these tubes function for more than 500 hours?
The probability that a certain kind of component will survive a given shock test is \[\frac{3}{4} .\] Find the probability that among 5 components tested exactly 2 will survive .
Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.2. If 6 bombs are dropped, find the probability that at least 2 will strike the target
It is known that 60% of mice inoculated with a serum are protected from a certain disease. If 5 mice are inoculated, find the probability that more than 3 contract the disease .
In a hospital, there are 20 kidney dialysis machines and the chance of any one of them to be out of service during a day is 0.02. Determine the probability that exactly 3 machines will be out of service on the same day.
The probability that a student entering a university will graduate is 0.4. Find the probability that out of 3 students of the university all will graduate .
The probability of a shooter hitting a target is \[\frac{3}{4} .\] How many minimum number of times must he/she fire so that the probability of hitting the target at least once is more than 0.99?
Find the binomial distribution when the sum of its mean and variance for 5 trials is 4.8.
If the probability of a defective bolt is 0.1, find the (i) mean and (ii) standard deviation for the distribution of bolts in a total of 400 bolts.
If on an average 9 ships out of 10 arrive safely at ports, find the mean and S.D. of the ships returning safely out of a total of 500 ships.
In eight throws of a die, 5 or 6 is considered a success. Find the mean number of successes and the standard deviation.
The probability that an item produced by a factory is defective is 0.02. A shipment of 10,000 items is sent to its warehouse. Find the expected number of defective items and the standard deviation.
If a random variable X follows a binomial distribution with mean 3 and variance 3/2, find P (X ≤ 5).
If in a binomial distribution n = 4 and P (X = 0) = \[\frac{16}{81}\] , find q.
One hundred identical coins, each with probability p of showing heads are tossed once. If 0 < p < 1 and the probability of heads showing on 50 coins is equal to that of heads showing on 51 coins, the value of p is
If the mean and variance of a binomial variate X are 2 and 1 respectively, then the probability that X takes a value greater than 1 is
In a binomial distribution, the probability of getting success is 1/4 and standard deviation is 3. Then, its mean is
For a binomial variate X, if n = 3 and P (X = 1) = 8 P (X = 3), then p =
Mark the correct alternative in the following question:
Suppose a random variable X follows the binomial distribution with parameters n and p, where 0 < p < 1. If \[\frac{P\left( X = r \right)}{P\left( X = n - r \right)}\] is independent of n and r, then p equals
Mark the correct alternative in the following question:
The probability of guessing correctly at least 8 out of 10 answers of a true false type examination is
A bag contains 7 red, 5 white and 8 black balls. If four balls are drawn one by one with replacement, what is the probability that any two are white ?
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs not more than one will fuse after 150 days of use
If x4 occurs in the tth term in the expansion of `(x^4 + 1/x^3)^15`, then the value oft is equal to:
If in the binomial expansion of (1 + x)n where n is a natural number, the coefficients of the 5th, 6th and 7th terms are in A.P., then n is equal to:
A pair of dice is thrown four times. If getting a doublet is considered a success then find the probability of two success.
If a fair coin is tossed 10 times. Find the probability of getting at most six heads.
A student is given a quiz with 10 true or false questions and he answers by sheer guessing. If X is the number of questions answered correctly write the p.m.f. of X. If the student passes the quiz by getting 7 or more correct answers what is the probability that the student passes the quiz?
If X ∼ B(n, p), n = 6 and 9 P(X = 4) = P(X = 2), then find the value of p.
