Advertisements
Advertisements
प्रश्न
An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be at least 4 successes.
उत्तर
The probability of success is twice the probability of failure.
Let the probability of failure be x.
∴ Probability of success = 2x
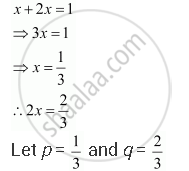
Let X be the random variable that represents the number of successes in six trials.
By binomial distribution, we obtain
P (X = x) = `""^nC_x P^(n-x) q^x`
Probability of at least 4 successes = P (X ≥ 4)
= P (X = 4) + P (X = 5) + P (X = 6)

APPEARS IN
संबंधित प्रश्न
The probability that a bomb will hit a target is 0.8. Find the probability that out of 10 bombs dropped, exactly 4 will hit the target.
In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5/6 . What is the probability that he will knock down fewer than 2 hurdles?
Five cards are drawn successively with replacement from a well-shuffled pack of 52 cards. What is the probability that all the five cards are spades ?
An urn contains four white and three red balls. Find the probability distribution of the number of red balls in three draws with replacement from the urn.
A card is drawn and replaced in an ordinary pack of 52 cards. How many times must a card be drawn so that (i) there is at least an even chance of drawing a heart (ii) the probability of drawing a heart is greater than 3/4?
Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.2. If 6 bombs are dropped, find the probability that at least 2 will strike the target
In a hospital, there are 20 kidney dialysis machines and the chance of any one of them to be out of service during a day is 0.02. Determine the probability that exactly 3 machines will be out of service on the same day.
In a 20-question true-false examination, suppose a student tosses a fair coin to determine his answer to each question. For every head, he answers 'true' and for every tail, he answers 'false'. Find the probability that he answers at least 12 questions correctly.
Suppose X has a binomial distribution with n = 6 and \[p = \frac{1}{2} .\] Show that X = 3 is the most likely outcome.
The probability of a shooter hitting a target is \[\frac{3}{4} .\] How many minimum number of times must he/she fire so that the probability of hitting the target at least once is more than 0.99?
A die is thrown 5 times. Find the probability that an odd number will come up exactly three times.
A factory produces bulbs. The probability that one bulb is defective is \[\frac{1}{50}\] and they are packed in boxes of 10. From a single box, find the probability that exactly two bulbs are defective
A factory produces bulbs. The probability that one bulb is defective is \[\frac{1}{50}\] and they are packed in boxes of 10. From a single box, find the probability that more than 8 bulbs work properly
Determine the binomial distribution whose mean is 20 and variance 16.
If X follows a binomial distribution with mean 4 and variance 2, find P (X ≥ 5).
If the sum of the mean and variance of a binomial distribution for 6 trials is \[\frac{10}{3},\] find the distribution.
A die is thrown three times. Let X be 'the number of twos seen'. Find the expectation of X.
In a group of 200 items, if the probability of getting a defective item is 0.2, write the mean of the distribution.
If the mean of a binomial distribution is 20 and its standard deviation is 4, find p.
If the mean and variance of a random variable X with a binomial distribution are 4 and 2 respectively, find P (X = 1).
In a box containing 100 bulbs, 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective?
A rifleman is firing at a distant target and has only 10% chance of hitting it. The least number of rounds he must fire in order to have more than 50% chance of hitting it at least once is
A fair coin is tossed a fixed number of times. If the probability of getting seven heads is equal to that of getting nine heads, the probability of getting two heads is
A fair coin is tossed 100 times. The probability of getting tails an odd number of times is
A five-digit number is written down at random. The probability that the number is divisible by 5, and no two consecutive digits are identical, is
A coin is tossed 10 times. The probability of getting exactly six heads is
In a binomial distribution, the probability of getting success is 1/4 and standard deviation is 3. Then, its mean is
For a binomial variate X, if n = 3 and P (X = 1) = 8 P (X = 3), then p =
Mark the correct alternative in the following question:
The probability of guessing correctly at least 8 out of 10 answers of a true false type examination is
Five cards are drawn successively with replacement from a well-shuffled pack of 52 cards. What is the probability that only 3 cards are spades ?
Five cards are drawn successively with replacement from a well-shuffled pack of 52 cards. What is the probability that none is a spade ?
Determine the binomial distribution where mean is 9 and standard deviation is `3/2` Also, find the probability of obtaining at most one success.
Find the mean and variance of the random variable X which denotes the number of doublets in four throws of a pair of dice.
For Bernoulli Distribution, state formula for E(X) and V(X).
For X ~ B(n, p) and P(X = x) = `""^8"C"_x(1/2)^x (1/2)^(8 - x)`, then state value of n and p
Explain why the experiment of tossing a coin three times is said to have binomial distribution.
The mean, median and mode for binomial distribution will be equal when
If a random variable X follows the Binomial distribution B (33, p) such that 3P(X = 0) = P(X = 1), then the value of `(P(X = 15))/(P(X = 18)) - (P(X = 16))/(P(X = 17))` is equal to ______.
