Advertisements
Advertisements
Question
An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be at least 4 successes.
Solution
The probability of success is twice the probability of failure.
Let the probability of failure be x.
∴ Probability of success = 2x
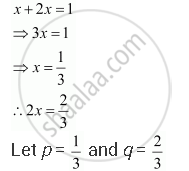
Let X be the random variable that represents the number of successes in six trials.
By binomial distribution, we obtain
P (X = x) = `""^nC_x P^(n-x) q^x`
Probability of at least 4 successes = P (X ≥ 4)
= P (X = 4) + P (X = 5) + P (X = 6)

APPEARS IN
RELATED QUESTIONS
Given that X ~ B(n= 10, p). If E(X) = 8 then the value of
p is ...........
(a) 0.6
(b) 0.7
(c) 0.8
(d) 0.4
Given X ~ B (n, p)
If n = 10 and p = 0.4, find E(X) and var (X).
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. What is the probability that out of 5 such bulbs
(i) none
(ii) not more than one
(iii) more than one
(iv) at least one, will fuse after 150 days of use.
Find the probability of getting 5 exactly twice in 7 throws of a die.
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
(A) 10−1
(B) `(1/2)^5`
(C) `(9/10)^5`
(D) 9/10
The probability that a student is not a swimmer is 1/5 . Then the probability that out of five students, four are swimmers is
(A) `""^5C_4 (4/5)^4 1/5`
(B) `(4/5)^4 1/5
(C) `""^5C_1 1/5 (4/5)^4 `
(D) None of these
The probability of a man hitting a target is 1/4. If he fires 7 times, what is the probability of his hitting the target at least twice?
Assume that on an average one telephone number out of 15 called between 2 P.M. and 3 P.M. on week days is busy. What is the probability that if six randomly selected telephone numbers are called, at least 3 of them will be busy?
Five cards are drawn successively with replacement from a well-shuffled pack of 52 cards. What is the probability that all the five cards are spades ?
In a large bulk of items, 5 percent of the items are defective. What is the probability that a sample of 10 items will include not more than one defective item?
It is known that 60% of mice inoculated with a serum are protected from a certain disease. If 5 mice are inoculated, find the probability that none contract the disease .
In a multiple-choice examination with three possible answers for each of the five questions out of which only one is correct, what is the probability that a candidate would get four or more correct answers just by guessing?
From a lot of 30 bulbs that includes 6 defective bulbs, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.
A factory produces bulbs. The probability that one bulb is defective is \[\frac{1}{50}\] and they are packed in boxes of 10. From a single box, find the probability that more than 8 bulbs work properly
In a binomial distribution the sum and product of the mean and the variance are \[\frac{25}{3}\] and \[\frac{50}{3}\]
respectively. Find the distribution.
If the probability of a defective bolt is 0.1, find the (i) mean and (ii) standard deviation for the distribution of bolts in a total of 400 bolts.
The mean and variance of a binomial distribution are \[\frac{4}{3}\] and \[\frac{8}{9}\] respectively. Find P (X ≥ 1).
If the mean of a binomial distribution is 20 and its standard deviation is 4, find p.
The mean of a binomial distribution is 10 and its standard deviation is 2; write the value of q.
If the mean and variance of a binomial distribution are 4 and 3, respectively, find the probability of no success.
If for a binomial distribution P (X = 1) = P (X = 2) = α, write P (X = 4) in terms of α.
A five-digit number is written down at random. The probability that the number is divisible by 5, and no two consecutive digits are identical, is
Determine the binomial distribution where mean is 9 and standard deviation is `3/2` Also, find the probability of obtaining at most one success.
For Bernoulli Distribution, state formula for E(X) and V(X).
One of the condition of Bernoulli trials is that the trials are independent of each other.
The mean, median and mode for binomial distribution will be equal when
If x4 occurs in the tth term in the expansion of `(x^4 + 1/x^3)^15`, then the value oft is equal to:
If the coefficients of x7 and x8 in `(2 + x/3)^n` are equal, then n is
If in the binomial expansion of (1 + x)n where n is a natural number, the coefficients of the 5th, 6th and 7th terms are in A.P., then n is equal to:
A box B1 contains 1 white ball and 3 red balls. Another box B2 contains 2 white balls and 3 red balls. If one ball is drawn at random from each of the boxes B1 and B2, then find the probability that the two balls drawn are of the same colour.
An ordinary dice is rolled for a certain number of times. If the probability of getting an odd number 2 times is equal to the probability of getting an even number 3 times, then the probability of getting an odd number for odd number of times is ______.
The mean and variance of a binomial distribution are α and `α/3` respectively. If P(X = 1) = `4/243`, then P(X = 4 or 5) is equal to ______.
If a random variable X follows the Binomial distribution B (33, p) such that 3P(X = 0) = P(X = 1), then the value of `(P(X = 15))/(P(X = 18)) - (P(X = 16))/(P(X = 17))` is equal to ______.
If X ∼ B(n, p), n = 6 and 9 P(X = 4) = P(X = 2), then find the value of p.
An experiment succeeds thrice as often as it fails. Then in next five trials, find the probability that there will be two successes.
