Advertisements
Advertisements
प्रश्न
Consider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
उत्तर
Let the total charge of the ring be Q.
Radius of the ring = R
The electric field at distance x from the centre of ring,
\[E = \frac{Qx}{4\pi \epsilon_0 \left( R^2 + x^2 \right)^{3/2}} . . . (1)\]
For maximum value of electric field,
\[\frac{dE}{dx} = 0\]
From equation (1),
\[\Rightarrow R^2 + x^2 - 3 x^2 = 0\]
\[ \Rightarrow 3 x^2 = R^2 \]
\[ \Rightarrow x = \frac{R}{\sqrt{2}}\]
APPEARS IN
संबंधित प्रश्न
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
Show that if we connect the smaller and the outer sphere by a wire, the charge q on the former will always flow to the latter, independent of how large the charge Q is.
Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
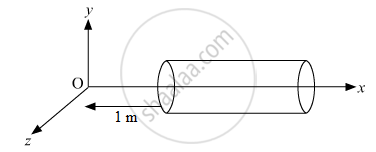
A hollow cylindrical box of length 0.5 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 20 xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
When the separation between two charges is increased, the electric potential energy of the charges
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
The electric field in a region is directed outward and is proportional to the distance rfrom the origin. Taking the electric potential at the origin to be zero,
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 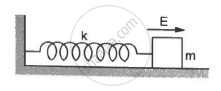
Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
In general, metallic ropes are suspended on the carriers taking inflammable materials. The reason is ______.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
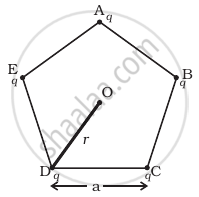
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
