Advertisements
Advertisements
प्रश्न
Find the change in the internal energy of 2 kg of water as it is heated from 0°C to 4°C. The specific heat capacity of water is 4200 J kg−1 K−1 and its densities at 0°C and 4°C are 999.9 kg m−3 and 1000 kg m−3 respectively. Atmospheric pressure = 105 Pa.
उत्तर
Given:-
Mass of water, M = 2 kg
Change in temperature of the system, ∆θ = 4°C = 277 K
Specific heat of water, sw = 4200 J/kg-°C
Initial density, p0 = 999.9 kg/m3
Final density, pf = 1000 kg/m3
P = 105 Pa
Let change in internal energy be ∆U.
Using the first law of thermodynamics, we get
∆Q = ∆U + ∆W
Also, ∆Q = ms∆θ
W = P∆V = P(Vf - Vi)
⇒ ms∆θ = ∆U + P (V0 − V4)
⇒ 2 × 4200 × 4= ∆U + 105 (∆V)
⇒ 33600 = ∆U + 105
\[\left( \frac{m}{p_0} - \frac{m}{p_f} \right)\]
⇒ 33600 = ∆U + 105 × ( - 0.0000002)
⇒ 33600 = ∆U - 0.02
∆U = (33600 - 0.02) J
APPEARS IN
संबंधित प्रश्न
When we heat an object, it expands. Is work done by the object in this process? Is heat given to the object equal to the increase in its internal energy?
A system can be taken from the initial state p1, V1 to the final state p2, V2 by two different methods. Let ∆Q and ∆W represent the heat given to the system and the work done by the system. Which of the following must be the same in both the methods?
Refer to figure. Let ∆U1 and ∆U2 be the change in internal energy in processes A and B respectively, ∆Q be the net heat given to the system in process A + B and ∆W be the net work done by the system in the process A + B.

(a) ∆U1 + ∆U2 = 0
(b) ∆U1 − ∆U2 = 0
(c) ∆Q − ∆W = 0
(d) ∆Q + ∆W = 0
Calculate the change in internal energy of a gas kept in a rigid container when 100 J of heat is supplied to it.
The pressure of a gas changes linearly with volume from 10 kPa, 200 cc to 50 kPa, 50 cc. (a) Calculate the work done by the gas. (b) If no heat is supplied or extracted from the gas, what is the change in the internal energy of the gas?
The internal energy of a gas is given by U = 1.5 pV. It expands from 100 cm3 to 200 cm3against a constant pressure of 1.0 × 105 Pa. Calculate the heat absorbed by the gas in the process.
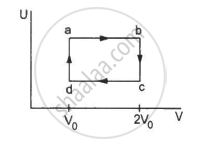
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
A resistor held in running water carries electric current. Treat the resistor as the system
- Does heat flow into the resistor?
- Is there a flow of heat into the water?
- Is any work done?
- Assuming the state of resistance to remain unchanged, apply the first law of thermodynamics to this process.
For an Isothermal process
A sample of gas absorbs 4000 kJ of heat and surrounding does 2000 J of work on sample. What is the value of ∆U?
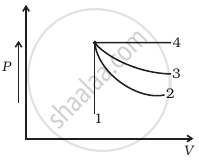
An ideal gas undergoes four different processes from the same initial state (figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4 which one is adiabatic.
An ideal gas undergoes cyclic process ABCDA as shown in given P-V diagram (figure). The amount of work done by the gas is ______.

Three copper blocks of masses M1, M2 and M3 kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at T1, T2, T3 (T1 > T2 > T3). Assuming there is no heat loss to the surroundings, the equilibrium temprature T is (s is specific heat of copper)
Air pressure in a car tyre increases during driving. Explain.
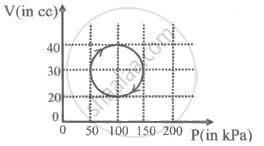
A system is taken through a cyclic process represented by a circle as shown. The heat absorbed by the system is ______.
200g water is heated from 40°C to 60°C. Ignoring the slight expansion of water, the change in its internal energy is close to ______.
(Given specific heat of water = 4184 J/kgK)
Mathematical equation of first law of thermodynamics for isochoric process is ______.
If one mole of monoatomic gas `(gamma=5/3)` is mixed with one mole of diatomic gas `(gamma=7/5)`, the value of γ for the mixture is ______.
In an adiabatic expansion of 2 moles of a gas, the initial pressure was 1.013 × 105 Pa, the initial volume was 22.4 L, the final pressure was 3.191 × 104 Pa and the final volume was 44.8 L. Find the work done by the gas on its surroundings. Taken `γ = 5/3`.
