Advertisements
Advertisements
प्रश्न
Maximize z = 5x + 2y subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
उत्तर
To draw the feasible region, construct table as follows:
| Inequality | 3x + 5y ≤ 15 | 5x + 2y ≤ 10 |
| Corresponding equation (of line) | 3x + 5y = 15 | 5x + 2y = 10 |
| Intersection of line with X-axis | (5, 0) | (2, 0) |
| Intersection of line with Y-axis | (0, 3) | (0, 5) |
| Region | Origin side | Origin side |
x ≥ 0, y ≥ 0 represent 1st quadrant.
Here, the objective function is Z = 5x + 2y
∴ Z at O(0, 0) = 5(0) + 2(0) = 0
Z at Q(2, 0) = 5(2) + 2(0) = 10
Z at R `(20/19, 45/19) = 5 (20/19) + 2(45/19) = 10`
Z at A(0, 3) = 5(0) + 2(3) = 6
The maximum value of Z is 10 and it occurs at every point lying on the line segment joining `"R"(20/19, 45/19)` and Q(2, 0).
Hence, there are infinitely many optimal solutions.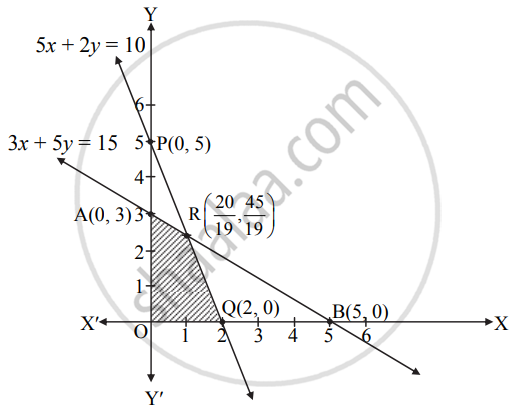
संबंधित प्रश्न
Find the feasible solution of the following inequation:
2x + 3y ≤ 6, x + y ≥ 2, x ≥ 0, y ≥ 0
A company produces two types of articles A and B which requires silver and gold. Each unit of A requires 3 gm of silver and 1 gm of gold, while each unit of B requires 2 gm of silver and 2 gm of gold. The company has 6 gm of silver and 4 gm of gold. Construct the inequations and find feasible solution graphically.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to the machine shop for finishing. The number of man-hours of labour required in each shop for production of A and B per unit and the number of man-hours available for the firm is as follows :
| Gadgets | Foundry | Machine shop |
| A | 10 | 5 |
| B | 6 | 4 |
| Time available (hour) | 60 | 35 |
Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 in magazines A and B per copy. These are processed on three Machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II, and 2 hours on machine III. Magazine B requires 3 hours on machine I, 2 hours on machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, and 60 hours per week respectively. Formulate the LPP to determine weekly production of magazines A and B, so that the total profit is maximum.
A manufacturer produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs requires 1 hour of work on Machine M1 and 3 hours of work on Machine M2. A package of tubes requires 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LPP to maximize the profit, if he operates the machine M1, for almost 10 hours a day and machine M2 for almost 12 hours a day.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be at least 5 kg. Cement costs ₹ 20 per kg and sand costs of ₹ 6 per kg. Strength consideration dictates that a concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand. Form the L.P.P. for the cost to be minimum.
Solve the following LPP by graphical method:
Maximize z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0
Minimize z = 6x + 2y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0.
Which of the following is correct?
The corner points of the feasible solution given by the inequation x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0 are ______.
The half-plane represented by 3x + 2y < 8 contains the point ______.
Solve the following LPP:
Maximize z = 5x1 + 6x2 subject to 2x1 + 3x2 ≤ 18, 2x1 + x2 ≤ 12, x1 ≥ 0, x2 ≥ 0.
Solve the following LPP:
Maximize z = 4x + 2y subject to 3x + y ≤ 27, x + y ≤ 21, x ≥ 0, y ≥ 0.
A chemical company produces a chemical containing three basic elements A, B, C, so that it has at least 16 litres of A, 24 litres of B and 18 litres of C. This chemical is made by mixing two compounds I and II. Each unit of compound I has 4 litres of A, 12 litres of B and 2 litres of C. Each unit of compound II has 2 litres of A, 2 litres of B and 6 litres of C. The cost per unit of compound I is ₹ 800 and that of compound II is ₹ 640. Formulate the problems as LPP and solve it to minimize the cost.
A firm manufactures two products A and B on which profit earned per unit ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. The product A requires one minute of processing time on M1 and two minutes of processing time on M2, B requires one minute of processing time on M1 and one minute of processing time on M2. Machine M1 is available for use for 450 minutes while M2 is available for 600 minutes during any working day. Find the number of units of product A and B to be manufactured to get the maximum profit.
A firm manufacturing two types of electrical items A and B, can make a profit of ₹ 20 per unit of A and ₹ 30 per unit of B. Both A and B make use of two essential components a motor and a transformer. Each unit of A requires 3 motors and 2 transformers and each units of B requires 2 motors and 4 transformers. The total supply of components per month is restricted to 210 motors and 300 transformers. How many units of A and B should be manufactured per month to maximize profit? How much is the maximum profit?
Solve the following L.P.P. by graphical method:
Maximize: Z = 4x + 6y
Subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Choose the correct alternative :
The corner points of the feasible region given by the inequations x + y ≤ 4, 2x + y ≤ 7, x ≥ 0, y ≥ 0, are
State whether the following is True or False :
The feasible solution of LPP belongs to only quadrant I.
The feasible region is the set of point which satisfy.
Which value of x is in the solution set of inequality − 2X + Y ≥ 17
Maximize z = 7x + 11y subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the Linear Programming problem graphically:
Maximize z = 3x + 5y subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0 also find the maximum value of z.
Minimize z = 7x + y subjected to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Minimize z = 2x + 4y is subjected to 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, y ≥ 0 show that the minimum value of z occurs at more than two points
x − y ≤ 1, x − y ≥ 0, x ≥ 0, y ≥ 0 are the constant for the objective function z = x + y. It is solvable for finding optimum value of z? Justify?
Choose the correct alternative:
Z = 9x + 13y subjected to constraints 2x + 3y ≤ 18, 2x + y ≤ 10, 0 ≤ x, y was found to be maximum at the point
The variables involved in LPP are called ______
A company produces two types of products say type A and B. Profits on the two types of product are ₹ 30/- and ₹ 40/- per kg respectively. The data on resources required and availability of resources are given below.
| Requirements | Capacity available per month | ||
| Product A | Product B | ||
| Raw material (kgs) | 60 | 120 | 12000 |
| Machining hours/piece | 8 | 5 | 600 |
| Assembling (man hours) | 3 | 4 | 500 |
Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problems by graphical method.
Maximize Z = 22x1 + 18x2 subject to constraints 960x1 + 640x2 ≤ 15360; x1 + x2 ≤ 20 and x1, x2 ≥ 0.
Solve the following linear programming problems by graphical method.
Minimize Z = 20x1 + 40x2 subject to the constraints 36x1 + 6x2 ≥ 108; 3x1 + 12x2 ≥ 36; 20x1 + 10x2 ≥ 100 and x1, x2 ≥ 0.
A solution which maximizes or minimizes the given LPP is called
The minimum value of the objective function Z = x + 3y subject to the constraints 2x + y ≤ 20, x + 2y ≤ 20, x > 0 and y > 0 is
A firm manufactures two products A and B on which the profits earned per unit are ₹ 3 and ₹ 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2, While B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hrs 30 minutes while M2 is available for 10 hrs during any working day. Formulate this problem as a linear programming problem to maximize the profit.
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Minimize Z = 200x1 + 500x2 subject to the constraints: x1 + 2x2 ≥ 10; 3x1 + 4x2 ≤ 24 and x1 ≥ 0, x2 ≥ 0.
Solve the following linear programming problem graphically.
Maximize Z = 3x1 + 5x2 subject to the constraints: x1 + x2 ≤ 6, x1 ≤ 4; x2 ≤ 5, and x1, x2 ≥ 0.
Which of the following can be considered as the objective function of a linear programming problem?
The point which provides the solution of the linear programming problem, Max.(45x + 55y) subject to constraints x, y ≥ 0, 6x + 4y ≤ 120, 3x + 10y ≤ 180, is ______
Solution which satisfy all constraints is called ______ solution.
Shamli wants to invest ₹ 50, 000 in saving certificates and PPF. She wants to invest atleast ₹ 15,000 in saving certificates and at least ₹ 20,000 in PPF. The rate of interest on saving certificates is 8% p.a. and that on PPF is 9% p.a. Formulation of the above problem as LPP to determine maximum yearly income, is ______.
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y Subject to: x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
Food F1 contains 2, 6, 1 units and food F2 contains 1, 1, 3 units of proteins, carbohydrates, fats respectively per kg. 8, 12 and 9 units of proteins, carbohydrates and fats is the weekly minimum requirement for a person. The cost of food F1 is Rs. 85 and food F2 is Rs. 40 per kg. Formulate the L.P.P. to minimize the cost.
