Advertisements
Advertisements
प्रश्न
Prove by vector method, that the angle subtended on semicircle is a right angle.
उत्तर १
Let seg AB be a diameter of a circle with centre C and P be any point on the circle other than A and B.
Then ∠APB is an angle subtended on a semicircle.
Let `bar"AC" = bar"CB" = bar"a"` and `bar"CP" = bar"r"`
Then `|bar"a"| = |bar"r"|` ....(1)

`bar"AP" = bar"AC" + bar"CP"`
= `bar"a" + bar"r"`
= `bar"r" + bar"a"`
`bar"BP" = bar"BC" + bar"CP"`
= `- bar"CB" + bar"CP"`
= `- bar"a" + bar"r"`
∴ `bar"AP".bar"BP" = (bar"r" + bar"a").(bar"r" - bar"a")`
= `bar"r".bar"r" - bar"r".bar"a" + bar"a".bar"r" - bar"a".bar"a"`
= `|bar"r"|^2 - |bar"a"|^2`
= 0 ....`(∵ bar"r".bar"a" = bar"a".bar"r")`
∴ `bar"AP" ⊥ bar"BP"`
∴ ∠APB is a right angle.
Hence, the angle subtended on a semicircle is the right angle.
उत्तर २
Consider the circle with the centre at O and AB is the diameter.
Let `bar(OA) = bar a, bar(OB) = bar b, bar(OC) = bar c`
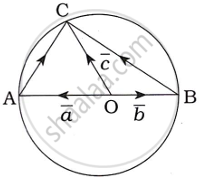
∴ `|bar a| =|bar b| = |bar c| = r` ...(1)
and `bar a = -bar b` ...(2)
Consider:
`bar (AC) * bar (BC) = (bar c - bar a) * (bar c - bar b)`
= `(bar c - bar a) * (bar c + bar a)` ...[From (2)]
= `|bar c|^2 - |bar a|^2`
= r2 − r2 ...[From (1)]
= 0
∴ `bar(AC) * bar(BC) = 0`
∴ `bar(AC)` is perpendicular to `bar(BC)`
∴ ∠ACB = 90°
∴ Angle subtended on semi-circle is a right angle.
APPEARS IN
संबंधित प्रश्न
If A, B, C, D are (1, 1, 1), (2, 1, 3), (3, 2, 2), (3, 3, 4) respectively, then find the volume of parallelopiped with AB, AC and AD as the concurrent edges.
Prove that the volume of a parallelopiped with coterminal edges as ` bara ,bar b , barc `
Hence find the volume of the parallelopiped with coterminal edges `bar i+barj, barj+bark `
If `bar c = 3bara- 2bar b ` Prove that `[bar a bar b barc]=0`
Show that the four points A(4, 5, 1), B(0, –1, –1), C(3, 9, 4) and D(–4, 4, 4) are coplanar.
Find λ, if the vectors `veca=hati+3hatj+hatk,vecb=2hati−hatj−hatk and vecc=λhatj+3hatk` are coplanar.
Find the volume of the parallelopiped whose coterminus edges are given by vectors
`2hati+3hatj-4hatk, 5hati+7hatj+5hatk and 4hati+5hatj-2hatk`
If `bara=3hati-hatj+4hatk, barb=2hati+3hatj-hatk, barc=-5hati+2hatj+3hatk` then `bara.(barbxxbarc)=`
(A) 100
(B) 101
(C) 110
(D) 109
Find the volume of a tetrahedron whose vertices are A(−1, 2, 3), B(3, −2, 1), C(2, 1, 3) and D(−1, −2, 4).
Find the value of λ, if four points with position vectors `3hati + 6hatj+9hatk`, `hati + 2hatj + 3hatk`,`2hati + 3hatj + hatk` and `4hati + 6hatj + lambdahatk` are coplanar.
Let `veca = hati + hatj + hatk = hati` and `vecc = c_1veci + c_2hatj + c_3hatk` then
1) Let `c_1 = 1` and `c_2 = 2`, find `c_3` which makes `veca, vecb "and" vecc`coplanar
2) if `c_2 = -1` and `c_3 = 1`, show that no value of `c_1`can make `veca, vecb and vecc` coplanar
if `bara = 3hati - 2hatj+7hatk`, `barb = 5hati + hatj -2hatk`and `barc = hati + hatj - hatk` then find `bara.(barbxxbarc)`
Show that the four points A, B, C and D with position vectors `4hati + 5hatj + hatk`, `-hatj-hatk`, `3hati + 9hatj + 4hatk` and `4(-hati + hatj + hatk)` respectively are coplanar
Find the volume of a parallelopiped whose edges are represented by the vectors:
`vec a = 2 hat i - 3 hat j - 4 hat k`, `vec b = hat i + 2 hat j - hat k` and `vec c = 3 hat i + hat j + 2 hatk`
Find the volume of the parallelopiped whose coterminus edges are given by vectors `2hati+5hatj-4hatk, 5hati+7hatj+5hatk and 4hati+5hatj-2hatk`
Evaluate the following:
\[\left[ 2 \hat{i}\hat{ j}\ \hat{k}\right] + \left[\hat{i}\hat{ k}\hat {j} \right] + \left[\hat{ k}\hat{ j} 2\hat{ i} \right]\]
Find \[\left[ \vec{a} \vec{b} \vec{c} \right]\] , when \[\vec{a} = 2 \hat{i} - 3 \hat{j} , \vec{b} = \hat{i} + \hat{j} - \hat{k} \text{ and } \vec{c} = 3 \hat{i} - \hat{k}\]
Find \[\left[ \vec{a} \vec{b} \vec{c} \right]\] , when \[\vec{a} =\hat{ i} - 2 \hat{j} + 3 \hat{k} , \vec{b} = 2 \hat{i} + \hat{j} - \hat{k}\text{ and } \vec{c} = \hat{j} + \hat{k}\]
Find the volume of the parallelopiped whose coterminous edges are represented by the vector:
\[\vec{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} , \vec{b} =\hat{ i} + 2 \hat{j} - \hat{k} , \vec{c} = 3 \hat{i} - \hat{j} + 2 \hat{k}\]
Find the volume of the parallelopiped whose coterminous edges are represented by the vector:
\[\vec{a} = 2 \hat{i} - 3 \hat{j} + 4 \hat{k} , \vec{b} = \hat{i} + 2 \hat{j} - \hat{k} , \vec{c} = 3 \hat{i} - \hat{j} - 2 \hat{k}\]
Find the volume of the parallelopiped whose coterminous edges are represented by the vector:
\[\vec{a} = 11 \hat{i} , \vec{b} = 2 \hat{j} , \vec{c} = 13 \hat{k}\]
Show of the following triad of vector is coplanar:
\[\vec{a} = \hat {i} + 2 \hat{j} - \hat {k} , \vec{b} = 3 \hat {i} + 2 \hat{j} + 7 \hat {k} , \vec{c} = 5 \hat {i} + 6 \hat { j} + 5 \hat {k}\]
Show of the following triad of vector is coplanar:
\[\hat{a} = \hat{i} - 2 \hat {j} + 3 \hat {k} , \hat {b} = - 2 \hat {i} + 3 \hat {j} - 4 \hat { k}, \hat {c} = \hat { i} - 3 \hat { j} + 5 \hat { k }\]
Find the value of λ so that the following vector is coplanar:
\[\vec{a} = \hat{i} - \hat{j} + \hat{k} , \vec{b} = 2 \hat {i} + \hat {j} - \hat {k} , \vec{c} = \lambda\hat { i} - \hat {j} + \lambda \hat {k}\]
Find the value of λ so that the following vector is coplanar:
\[\vec{a} = 2 \hat{i} - \hat {j} + \hat {k} , \vec{b} = \hat {i} + 2 \hat {j} - 3 \hat {k} , \vec{c} = \lambda \hat {i} + \lambda \hat {j} + 5 \hat {k}\]
Find the value of λ so that the following vector is coplanar:
\[\vec{a} = \hat {i} + 3 \hat {j} , \vec{b} = 5 \hat {k} , \vec{c} = \lambda \hat {i} - \hat {j}\]
Show that the points A (−1, 4, −3), B (3, 2, −5), C (−3, 8, −5) and D (−3, 2, 1) are coplanar.
Show that four points whose position vectors are
\[6 \hat { i} - 7 \hat {j} , 16 \hat { i} - 19 \hat { j} - 4 \hat {k} , 3 \hat {i} - 6 \hat {k} , 2 \hat { i} - 5 \hat {j}+ 10 \hat {k}\]
Find the value of λ for which the four points with position vectors
\[-\hat { j} - \hat {k} , 4 \hat {i} + 5 \hat {j} + \lambda \hat {k} , 3 \hat {i} + 9 \hat {j} + 4 \hat {k} \text { and } - 4 \hat {i} + 4 \hat {j} + 4 \hat{k}\]
\[\text {Let } \vec{a} = \hat {i} + \hat {j} + \hat {k} , \vec{b} = \hat {i} \text{and} \hat {c} = c_1 \hat{i} + c_2 \hat {j} + c_3 \hat {k} . \text {Then},\]
If c1 = 1 and c2 = 2, find c3 which makes \[\vec{a,} \vec{b} \text { and } \vec{c}\] coplanar.
\[\text {Let } \vec{a} = \hat {i} + \hat {j} + \hat {k} , \vec{b} = \hat {i} \text{ and } \hat {c} = c_1 \hat{i} + c_2 \hat {j} + c_3 \hat {k} . \text {Then},\]
If c2 = −1 and c3 = 1, show that no value of c1 can make \[\vec{a,} \vec{b}\text { and } \vec{c}\] coplanar.
Find λ for which the points A (3, 2, 1), B (4, λ, 5), C (4, 2, −2) and D (6, 5, −1) are coplanar.
If four points A, B, C and D with position vectors 4 \[\hat { i} +3\] \[\hat { j} +3\] \[\hat { k} ,5\] \[\hat { i} +\] \[x\hat { j} +7\] \[\hat { k} ,5\] \[\hat { i} +3\] \[\hat { j}\] and \[7 \hat{i} + 6 \hat{j} + \hat{k}\] respectively are coplanar, then find the value of x.
Write the value of \[\left[ \hat {i} - \hat {j} \hat {j} - \hat {k} \hat {k} - \hat {i} \right] .\]
Find the values of 'a' for which the vectors
\[\vec{\alpha} = \hat {i} + 2 \hat {j} + \hat {k} , \vec{\beta} = a \hat {i} + \hat {j} + 2 \hat {k} \text { and } \vec{\gamma} = \hat {i} + 2 \hat {j} + a \hat { k }\] are coplanar.
If \[\vec{a,} \vec{b}\] \[\text { are non-collinear vectors, then find the value of} \left[ \vec{a} \vec{b}\hat { i} \right] \hat{i} + \left[ \vec{a} \vec{b} \hat {j} \right] \hat {j} + \left[ \vec{a} \vec{b} \hat {k} \right] \hat {k} .\]
For any two vectors \[\vec{a} \text { and } \vec{b}\] of magnitudes 3 and 4 respectively, write the value of \[\left[ \vec{a} \vec{b} \vec{a} \times \vec{b} \right] + \left( \vec{a} \cdot \vec{b} \right)^2 .\]
If \[\left[ 3 \vec{a} + 7 \vec{b} \vec{c} \vec{d} \right] = \lambda\left[ \vec{a} \vec{c} \vec{d} \right] + \mu\left[ \vec{b} \vec{c} \vec{d} \right],\] then find the value of λ + μ.
If \[\vec{a,} \vec{b,} \vec{c}\] are non-coplanar vectors, then find the value of \[\frac{\vec{a} \cdot \left( \vec{b} \times \vec{c} \right)}{\left( \vec{c} \times \vec{a} \right) \cdot \vec{b}} + \frac{\vec{b} \cdot \left( \vec{a} \times \vec{c} \right)}{\vec{c} \cdot \left( \vec{a} \times \vec{b} \right)}\].
If \[\vec{a}\] lies in the plane of vectors \[\vec{b} \text { and } \vec{c}\], then which of the following is correct?
The value of \[\left[ \vec{a} - \vec{b} , \vec{b} - \vec{c} , \vec{c} - \vec{a} \right], \text { where } \left| \vec{a} \right| = 1, \left| \vec{b} \right| = 5, \left| \vec{c} \right| = 3, \text { is }\]
If \[\vec{r} \cdot \vec{a} = \vec{r} \cdot \vec{b} = \vec{r} \cdot \vec{c} = 0\] for some non-zero vector \[\vec{r} ,\] then the value of \[\left[ \vec{a} \vec{b} \vec{c} \right],\] is
If \[\vec{a,} \vec{b,} \vec{c}\] are non-coplanar vectors, then \[\frac{\vec{a} \cdot \left( \vec{b} \times \vec{c} \right)}{\left( \vec{c} \times \vec{a} \right) \cdot \vec{b}} + \frac{\vec{b} \cdot \left( \vec{a} \times \vec{c} \right)}{\vec{c} \cdot \left( \vec{a} \times \vec{b} \right)}\] is equal to
If \[\left[ 2 \vec{a} + 4 \vec{b} \vec{c} \vec{d} \right] = \lambda\left[ \vec{a} \vec{c} \vec{d} \right] + \mu\left[ \vec{b} \vec{c} \vec{d} \right],\] then λ + μ =
\[\left[ \vec{a} \vec{b} \vec{a} \times \vec{b} \right] + \left( \vec{a} . \vec{b} \right)^2 =\]
If the vectors \[4 \hat { i} + 11 \hat {j} + m \hat {k} , 7 \hat { i} + 2 \hat { j} + 6 \hat {k} \text { and } \hat {i} + 5 \hat {j} + 4 \hat {k}\] are coplanar, then m =
For non-zero vectors \[\vec{a,} \vec{b} \text { and }\vec{c}\] the relation \[\left| \left( \vec{a} \times \vec{b} \right) \cdot \vec{c} \right| = \left| \vec{a} \right| \left| \vec{b} \right| \left| \vec{c} \right|\] holds good, if
\[\left( \vec{a} + \vec{b} \right) \cdot \left( \vec{b} + \vec{c} \right) \times \left( \vec{a} + \vec{b} + \vec{c} \right) =\]
Find the volume of the parallelopiped, if the coterminus edges are given by the vectors `2hat"i" + 5hat"j" -4 hat"k", 5hat"i" +7hat"j"+5 hat "k" , 4hat"i" +5hat"j" - 2 hat"k"`.
Find the value of p, if the vectors `hat"i" - 2hat"j" + hat"k", 2hat"i" -5hat"j"+"p" hat "k" , 5hat"i" -9hat"j" + 4 hat"k"` are coplanar.
Show that the vectors `hat (i) - 2 hat(j) + 3 hat (k), - 2 hat(i) + 3 hat(j) - 4 hat(k) " and " hat(i) - 3 hat(j) + 5 hat(k) ` are coplanar.
Determine where `bar"a"` and `bar"b"` are orthogonal, parallel or neithe:
`bar"a" = - 9hat"i" + 6hat"j" + 15hat"k"` , `bar"b" = 6hat"i" - 4hat"j" - 10hat"k"`.
Determine where `bar"a"` and `bar"b"` are orthogonal, parallel or neithe:
`bar"a" = 2hat"i" + 3hat"j" - hat"k"` , `bar"b" = 5hat"i" - 2hat"j" + 4hat"k"`
Determine where `bb(bara)` and `bb(barb)` are orthogonal, parallel or neither.
`bara = -3/5hati + 1/2hatj + 1/3hatk , barb = 5hati + 4hatj + 3hatk`
Determine where `bar"a"` and `bar"b"` are orthogonal, parallel or neithe:
`bar"a" = 4hat"i" - hat"j" + 6hat"k"` , `bar"b" = 5hat"i" - 2hat"j" + 4hat"k"`
If a line has the direction ratios 4, −12, 18, then find its direction cosines
Find the angle between the lines whose direction cosines l, m, n satisfy the equations 5l + m + 3n = 0 and 5mn − 2nl + 6lm = 0.
If `bar"u" = hat"i" - 2hat"j" + hat"k" , bar"v" = 3hat"i" + hat"k"` and `bar"w" = hat"j" - hat"k"` are given vectors, then find `(bar"u" + bar"w").[(bar"u" xx bar"v") xx (bar"v" xx bar"w")]`
Using properties of scalar triple product, prove that `[(bar"a" + bar"b", bar"b" + bar"c", bar"c" + bar"a")] = 2[(bar"a", bar"b", bar"c")]`.
If `vec"a" = hat"i" - 2hat"j" + 3hat"k", vec"b" = 2hat"i" + hat"j" - 2hat"k", vec"c" = 3hat"i" + 2hat"j" + hat"k"`, find `vec"a" * (vec"b" xx vec"c")`
Find the volume of the parallelepiped whose coterminous edges are represented by the vectors `- 6hat"i" + 14hat"j" + 10hat"k", 14hat"i" - 10hat"j" - 6hat"k"` and `2hat"i" + 4hat"j" - 2hat"k"`
The volume of the parallelepiped whose coterminus edges are `7hat"i" + lambdahat"j" - 3hat"k", hat"i" + 2hat"j" - hat"k", -3hat"i" + 7hat"j" + 5hat"k"` is 90 cubic units. Find the value of λ
If `vec"a", vec"b", vec"c"` are three non-coplanar vectors represented by concurrent edges of a parallelepiped of volume 4 cubic units, find the value of `(vec"a" + vec"b") * (vec"b" xx vec"c") + (vec"b" + vec"c")* (vec"c" xx vec"a") + (vec"c" + vec"a") * (vec"a" xx vec"b")`
Find the altitude of a parallelepiped determined by the vectors `vec"a" = - 2hat"i" + 5hat"j" + 3hat"k", vec"b" = hat"i" + 3hat"j" - 2hat"k"` and `vec"c" = - vec"i" + vec"j" + 4vec"k"` if the base is taken as the parallelogram determined by `vec"b"` and `vec"c"`
If `vec"a" = hat"i" - hat"k", vec"b" = xhat"i" + hat"j" + (1 - x)hat"k", vec"c" = yhat"i" + xhat"j" + (1 + x - y)hat"k"`, show that `[(vec"a", vec"b", vec"c")]` depends on neither x nor y
If the vectors `"a"hat"i" + "a"hat"j" + "c"hat"k", hat"i" + hat"k"` and `"c"hat"i" + "c"hat"j" + "b"hat"k"` are coplanar, prove that c is the geometric mean of a and b
Let `vec"a", vec"b", vec"c"` be three non-zero vectors such that `vec"c"` is a unit vector perpendicular to both `vec"a"` and `vec"b"`. If the angle between `vec"a"` and `vec"b"` is `pi/6`, show that `[(vec"a", vec"b", vec"c")]^2 = 1/4|vec"a"|^2|vec"b"|^2`
The volume of tetrahedron whose vertices are A(3, 7, 4), B(5, -2, 3), C(-4, 5, 6), D(1, 2, 3) is ______.
If the scalar triple product of the vectors `-3hat"i" + 7hat"j" - 3hat"k", 3hat"i" - 7hat"j" + lambdahat"k" and 7hat"i" - 5hat"j" - 5hat"j"` is 272 then λ = ______.
If the volume of tetrahedron whose vertices are A(0, 1, 2), B(2, -3, 0), C(1, 0, 2) and D(-2,-3,lambda) is `7/3` cu.units, then the value of λ is ______.
If θ is the angle between the unit vectors `bar"a"` and `bar"b"`, the `cos theta = theta/2` = ______.
If `veca = hati + hatj + hatk, veca.vecb` = 1 and `veca xx vecb = hatj - hatk`, then find `|vecb|`.
Prove that the volume of a tetrahedron with coterminus edges `overlinea, overlineb` and `overlinec` is `1/6[(overlinea, overlineb, overlinec)]`.
Hence, find the volume of tetrahedron whose coterminus edges are `overlinea = hati + 2hatj + 3hatk, overlineb = -hati + hatj + 2hatk` and `overlinec = 2hati + hatj + 4hatk`.
Determine whether `bb(bara and barb)` are orthogonal, parallel or neither.
`bar a = -3/5hati + 1/2hatj + 1/3hatk, barb = 5hati + 4hatj + 3hatk`
If `2hati + 3hatj, hati + hatj + hatk` and `λhati + 4hatj + 2hatk` taken in order are coterminous edges of a parallelopiped of volume 2 cu. units, then find the value of λ.
Find the volume of the parallelopiped whose coterminous edges are `2hati - 3hatj, hati + hatj - hatk` and `3hati - hatk`.
If the points A(1, 2, 3), B(–1, 1, 2), C(2, 3, 4) and D(–1, x, 0) are coplanar find the value of x.
If `barc = 3bara - 2barb` and `[bara barb + barc bara + barb + barc]` = 0 then prove that `[bara barb barc]` = 0
Determine whether `bara and barb` are orthogonal, parallel or neither.
`bara = -3/5hati + 1/2hatj +1/3 hatk, barb = 5hati + 4hatj +3hatk`
If `u=hati -2hatj + hatk, barr=3hati + hatk and w=hatj, hatk` are given vectors, then find `[baru + barw]. [(barw xx barr)xx(barr xx barw)]`
Find the volume of a tetrahedron whose vertices are A(−1, 2, 3) B(3, −2, 1), C (2, 1, 3) and D(−1, −2, 4).
Determine whether `\bb(bara and barb)` are orthogonal, parallel or neither.
`bara = -3/5 hati + 1/2 hatj + 1/3 hatk, barb = 5hati + 4hatj + 3hatk `
Determine whether `bara and barb` are orthogonal, parallel or neither.
`bara = -3/5 hati + 1/2 hatj + 1/3 hatk, barb = 5 hati + 4 hatj + 3 hatk`
