Advertisements
Advertisements
प्रश्न
Prove that:
`(cos^2 "A")/(cos "A" - sin "A") + (sin "A")/(1 - cot "A")` = sin A + cos A
उत्तर
LHS = `(cos^2 "A")/(cos "A" - sin "A") + (sin "A")/(1 - cot "A")`
`= (cos^2 "A")/(cos "A" - sin "A") + (sin "A")/(1 - (cos "A")/(sin "A"))`
`= (cos^2 "A")/(cos "A" - sin "A") + (sin "A")/((sin "A" - cos "A")/(sin "A"))`
`= (cos^2 "A")/(cos "A" - sin "A") + (sin^2 "A")/ (sin "A" - cos "A")`
`= (cos^2 "A")/(cos "A" - sin "A") - (sin^2 "A")/(cos "A" - sin "A")`
`= (cos^2 "A" - sin^2 "A")/(cos "A" - sin "A")`
`= ((cos "A" + sin "A")(cos "A" - sin "A"))/((cos "A" - sin "A"))`
= sin A + cos A ...(RHS)
APPEARS IN
संबंधित प्रश्न
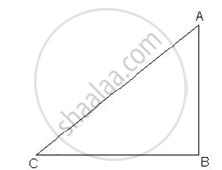
In the below given figure, a tower AB is 20 m high and BC, its shadow on the ground, is 20√3 m long. Find the sun’s altitude.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined:
(cosec A - sin A) (sec A - cos A) = `1/(tanA+cotA)`
[Hint: Simplify LHS and RHS separately.]
Without using trigonometric tables, evaluate :
`cot 38^circ/tan 52^circ`
Without using trigonometric tables, prove that:
cos 81° − sin 9° = 0
Without using trigonometric tables, prove that:
cosec272° − tan218° = 1
Prove that:
`(2 "sin" 68^circ)/(cos 10^circ )- (2 cot 15^circ)/(5 tan 75^circ) = ((3 tan 45^circ t an 20^circ tan 40^circ tan 50^circ tan 70^circ)) /5= 1`
Prove that:
cos1° cos2° cos3° ... cos180° = 0
If sin 3 A = cos (A − 26°), where 3 A is an acute angle, find the value of A.
Using trigonometric table evaluate the following:
tan 78°55' - tan 55°18'
Given that sin θ = `a/b` then cos θ is equal to ______.
