Advertisements
Advertisements
प्रश्न
The area of a triangle with vertices A, B, C is given by ______.
पर्याय
`|vec("AB") xx vec("AC")|`
`1/2|vec("AB") xx vec("AC")|`
`1/4|vec("AC") xx vec("AB")|`
`1/8|vec("AC") xx vec("AB")|`
उत्तर
The area of a triangle with vertices A, B, C is given by `underline(bb(1/2|vec(AB) xx vec(AC)|))`.
Explanation:
The area of the parallelogram with adjacent sides AB and AC = `|vec("AB") xx vec("AC")|`. Hence, the area of the triangle with vertices A, B, C = `1/2|vec("AB") xx vec("AC")|`
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If the points A(x, 2), B(−3, −4) and C(7, − 5) are collinear, then the value of x is:
(A) −63
(B) 63
(C) 60
(D) −60
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the following figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of Δ PQR if C is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find equation of line joining (1, 2) and (3, 6) using the determinant.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if `1/a+1/b=1`
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Find the area of ΔABC whose vertices are:
A(-5,7) , B (-4,-5) and C (4,5)
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
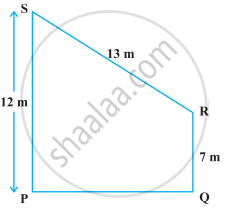
Find the area of the trapezium PQRS with height PQ given in the following figure.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

