Advertisements
Advertisements
Question
A first-order reaction is 50% complete in 30 minutes at 300 K and in 10 minutes at 320 K. Calculate activation energy (Ea) for the reaction. [R = 8.314 J K−1 mol−1]
[Given: log 2 = 0.3010, log 3 = 0.4771, log 4 = 0.6021]
Solution
Given: T1/2 = 30 min, T1 = 300 K
T1/2 = 10 min, T2 = 320 K
Formula: `log "K"_2/"K"_1 = "E"_"a"/(2.303 "R") [1/"T"_1 - 1/"T"_2]`
K = `0.693/("t"_(1//2))`
K1 at 300 K = `0.693/30` min−1
K2 at 320 K = `0.693/10` min−1
`log ("K"_2/"K"_1) = "E"_"a"/(2.303 "R") [1/"T"_1 - 1/"T"_2]`
`log ((0.693/10)/(0.693/30)) = "E"_"a"/(2.303 "R") [1/300 - 1/320]`
log (3) = `"E"_"a"/(2.303 "R") [20/(300 xx 320)]`
Ea = 0.4771 × 2.303 × 8.314 × 300 × 16
Ea = 43.8 kJ
APPEARS IN
RELATED QUESTIONS
(b) Rate constant ‘k’ of a reaction varies with temperature ‘T’ according to the equation:
`logk=logA-E_a/2.303R(1/T)`
Where Ea is the activation energy. When a graph is plotted for `logk Vs. 1/T` a straight line with a slope of −4250 K is obtained. Calculate ‘Ea’ for the reaction.(R = 8.314 JK−1 mol−1)
Consider a certain reaction \[\ce{A -> Products}\] with k = 2.0 × 10−2 s−1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L−1.
The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
In the Arrhenius equation for a first order reaction, the values of ‘A’ of ‘Ea’ are 4 x 1013 sec-1 and 98.6 kJ mol-1 respectively. At what temperature will its half life period be 10 minutes?
[R = 8.314 J K-1 mol-1]
The rate of chemical reaction becomes double for every 10° rise in temperature because of ____________.
Consider figure and mark the correct option.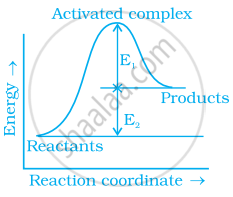
The reaction between \[\ce{H2(g)}\] and \[\ce{O2(g)}\] is highly feasible yet allowing the gases to stand at room temperature in the same vessel does not lead to the formation of water. Explain.
Why does the rate of a reaction increase with rise in temperature?
Oxygen is available in plenty in air yet fuels do not burn by themselves at room temperature. Explain.
The activation energy of one of the reactions in a biochemical process is 532611 J mol–1. When the temperature falls from 310 K to 300 K, the change in rate constant observed is k300 = x × 10–3 k310. The value of x is ______.
[Given: ln 10 = 2.3, R = 8.3 J K–1 mol–1]
