Advertisements
Advertisements
Question
A function f is defined as follows: f(x) = 4x + 5, for −4 ≤ x < 0. Find the values of f(−1), f(−2), f(0), if they exist.
Solution
f(x) = 4x + 5, – 4 ≤ x < 0
f(–1) = 4(–1) + 5 = –4 + 5 = 1
f(–2) = 4(–2) + 5 = –8 + 5 = –3
x = 0 ∉ domain of f
∴ f(0) does not exist.
APPEARS IN
RELATED QUESTIONS
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
If f(x) = (a − xn)1/n, a > 0 and n ∈ N, then prove that f(f(x)) = x for all x.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
f is a real valued function given by \[f\left( x \right) = 27 x^3 + \frac{1}{x^3}\] and α, β are roots of \[3x + \frac{1}{x} = 12\] . Then,
If ƒ(m) = m2 − 3m + 1, find f(x + 1)
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Check if the following relation is a function.
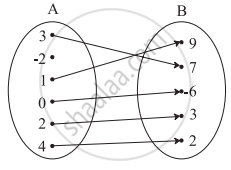
Find the domain and range of the following function.
f(x) = `sqrt((x - 2)(5 - x)`
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Prove that `"b"^(log_"b""a"` = a
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Domain of function f(x) = cos–1 6x is ______.
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
Find the domain of the following functions given by f(x) = x|x|
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
