Advertisements
Advertisements
Question
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Solution
`log ("pq"/"rs")` = log (pq) – log (rs) ...`[log "m"/"n" = log"m" - log"n"]`
= log p + log q – (log r + log s) ...[log mn = log m log n]
= log p + log q – log r – log s
APPEARS IN
RELATED QUESTIONS
f, g, h are three function defined from R to R as follow:
(i) f(x) = x2
Find the range of function.
If f(x) = (a − xn)1/n, a > 0 and n ∈ N, then prove that f(f(x)) = x for all x.
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
Let f(x) = x2 and g(x) = 2x+ 1 be two real functions. Find (f + g) (x), (f − g) (x), (fg) (x) and \[\left( \frac{f}{g} \right) \left( x \right)\] .
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
If f : R → R be given by for all \[f\left( x \right) = \frac{4^x}{4^x + 2}\] x ∈ R, then
The domain of the function
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
A function f is defined as follows: f(x) = 5 − x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Prove that `"b"^(log_"b""a"` = a
If f(x) = ax2 − bx + 6 and f(2) = 3 and f(4) = 30, find a and b
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
Answer the following:
A function f : R → R defined by f(x) = `(3x)/5 + 2`, x ∈ R. Show that f is one-one and onto. Hence find f–1
Answer the following:
Let f : R – {2} → R be defined by f(x) = `(x^2 - 4)/(x - 2)` and g : R → R be defined by g(x) = x + 2. Examine whether f = g or not
Answer the following:
Find x, if x = 33log32
Answer the following:
Show that, `log |sqrt(x^2 + 1) + x | + log | sqrt(x^2 + 1) - x|` = 0
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
Given the function f: x → x2 – 5x + 6, evaluate f(– 1)
A graph representing the function f(x) is given in it is clear that f(9) = 2
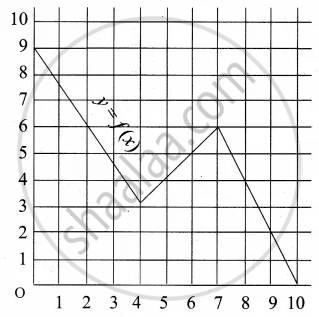
Describe the following Domain
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, find the range of f
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
Find the domain of the following functions given by f(x) = x|x|
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
Range of f(x) = `1/(1 - 2 cosx)` is ______.
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
The range of the function y = `1/(2 - sin3x)` is ______.
The range of the function f(x) = x2 + 2x+ 2 is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
