Advertisements
Advertisements
Question
A solution of \[\ce{Ni(NO3)2}\] is electrolysed between platinum electrodes using a current of 5 amperes for 20 minutes. What mass of \[\ce{Ni}\] is deposited at the cathode?
Solution
The reaction takes place in the following manner-
\[\ce{Ni^{2+} + 2e^- -> Ni}\]
Atomic weight of \[\ce{Ni}\] = 58.70
Equivalent weight of \[\ce{Ni}\] = `("atomic weight")/("number of valence electrons")`
= `58.70/2`
= 29.35
According to Faraday's first law of electrolysis,
W = `"Z"."I"."t" = "Equivalent weight"/96500 xx "I" xx "t"`
= `29.35/96500 xx 5 xx 20 xx 60`
= 1.825 g
APPEARS IN
RELATED QUESTIONS
On calculating the strength of current in amperes if a charge of 840C (coulomb) passes through an electrolyte in 7 minutes, it will be
- 1
- 2
- 3
- 4
The charge of how many coulomb is required to deposit 1.0 g of sodium metal (molar mass 23.0 g mol-1) from sodium ions is -
- 2098
- 96500
- 193000
- 4196
State the first law of electrolysis
Consider the reaction: \[\ce{Cr2O^{2-}_7 + 14H^+ + 6e^- -> 2Cr^{3+} + 7H2O}\]
What is the quantity of electricity in coulombs needed to reduce 1 mol of \[\ce{Cr2O^{2-}_7}\]?
How much charge is required for the following reduction:
1 mol of \[\ce{Al^{3+}}\] to \[\ce{Al}\]?
How much charge is required for the following reduction:
1 mol of \[\ce{Cu^{2+}}\] to \[\ce{Cu}\]?
Three electrolytic cells A, B, C containing solutions of \[\ce{ZnSO4}\], \[\ce{AgNO3}\] and \[\ce{CuSO4}\], respectively, are connected in series. A steady current of 1.5 amperes was passed through them until 1.45 g of silver deposited at the cathode of cell B. How long did the current flow? What mass of copper and zinc were deposited?
On passing 1.5 F charge, the number of moles of aluminium deposited at cathode are _______ [Molar mass of Al = 27 gram mol–1]
(A) 1.0
(B) 13.5
(C) 0.50
(D) 0.75
Calculate the mass of Ag deposited at cathode when a current of 2 amperes was passed through a solution of AgNO3 for 15 minutes.
(Given : Molar mass of Ag = 108 g mol−1 lF = 96500 C mol−1)
Solve the following question.
A steady current of 2 amperes was passed through two electrolytic cells X and Y connected in series containing electrolytes FeSO4 and ZnSO4 until 2.8 g of Fe deposited at the cathode of cell X. How long did the current flow? Calculate the mass of Zn deposited at the cathode of cell Y.
(Molar mass : Fe = 56 g mol–1, Zn = 65.3 g mol–1, 1F = 96500 C mol–1)
What will happen during the electrolysis of aqueous solution of \[\ce{CuSO4}\] by using platinum electrodes?
(i) Copper will deposit at cathode.
(ii) Copper will deposit at anode.
(iii) Oxygen will be released at anode.
(iv) Copper will dissolve at anode.
Aqueous copper sulphate solution and aqueous silver nitrate solution are electrolysed by 1 ampere current for 10 minutes in separate electrolytic cells. Will the mass of copper and silver deposited on the cathode be same or different? Explain your answer.
Consider the figure and answer the following question.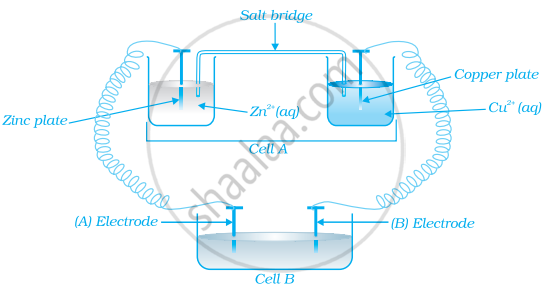
Cell ‘A’ has ECell = 2V and Cell ‘B’ has ECell = 1.1V which of the two cells ‘A’ or ‘B’ will act as an electrolytic cell. Which electrode reactions will occur in this cell?
Time Required to deposite one millimole of aluminium metal by the passage of 9.65 ampere through aqueous solution of aluminium is
Given `1/a` = 0.5 CM–1, R = 50 ohm, N = 1.0 then equivalent conductance of electrolytic cell is
Through an aqueous solution of an unknown salt of metal M (M = 200 g/mol) a current of 1.93 A is passed for 50 min. If 4 g of metal is produced at cathode. The charge on metal ion in solution is ______.
A current of 4 amp was passed for 2 hours through a solution of copper sulphate when 5.0 g of copper was deposited. The current efficiency is ______% (Cu = 63.5).
Assertion (A): During electrolysis of aqueous copper sulphate solution using copper electrodes hydrogen gas is released at the cathode.
Reason (R): The electrode potential of Cu2+/Cu is greater than that of H+/H2.
Select the most appropriate answer from the options given below:
How much electricity in terms of Faraday is required to produce 40.0 g of \[\ce{Al}\] from molten \[\ce{Al2O3}\]?
(Given: Molar mass of Aluminium is 27 g mol−1.)
