Advertisements
Advertisements
Question
Answer the following question.
Derive the relation between three coefficients of thermal expansion.
Solution
- Consider a square plate of side l0 at 0° C and lT at T °C.
∴ lT = l0 (1 + αT)
If area of plate at 0° C is A0, A0 = `l_0^2`
If area of plate at T °C is AT,
`"A"_"T" = l_1^2 = l_0^2 (1 +alpha"T")^2`
or `"A"_"T" = "A"_0(1 + alpha"T")^2` ....(1)
Also,
`"A"_"T" = "A"_0(1 + beta"T")` ....(2) `[because beta = ("A"_"r" - "A"_0)/("A"_0("T" - "T"_0))]` - Using Equations (1) and (2),
`"A"_0(1 + alpha"T")^2 = "A"_0(1 + beta"T")`
∴ `1 + 2alpha"T" + alpha^2"T"^2 = 1 + beta"T"` - Since the values of α are very small, the term α2T2 is very small and may be neglected.
∴ β = 2α - The result is general because any solid can be regarded as a collection of small squares.
- Consider a cube of side l0 at 0 °C and lT at T °C.
∴ lT = l0(1 + αT)
If volume of the cube at 0 °C is V0, V0 = `l_0^3`
If volume of the cube at T °C is
`"V"_"T", "V"_"T" = l_"T"^3 = l_0^3 (1 + alpha"T")^3`
`"V"_"T" = "V"_0(1 + alpha"T")^3` ....(1)
Also,
`"V"_"T" = "V"_0(1 + gamma"T")` ....(2) ...`[therefore gamma = ("V"_"T" - "V"_0)/("V"_0("T" - "T"_0))]` - Using Equations (1) and (2),
`"V"_0 (1 + alpha"T")^3 = "V"_0(1 + gamma"T")`
∴ `1 + 3alpha"T" + 3alpha^2"T"^2 + alpha^3"T"^3 = 1 + gamma"T"` - Since the values of α are very small, the terms with higher powers of α may be neglected.
∴ γ = 3α - The result is general because any solid can be regarded as a collection of small cubes.
- Relation between α, β and γ is given by,
`alpha = beta/2 = gamma/3`
where, α = coefficient of linear expansion,
β = coefficient of superficial expansion,
γ = coefficient of cubical expansion.
APPEARS IN
RELATED QUESTIONS
A steel tape 1m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is 27.0 °C? Coefficient of linear expansion of steel = 1.20 × 10–5 K–1
A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings Specific heat of aluminium = 0.91 J g–1 K–1
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
For a constant-volume gas thermometer, one should fill the gas at
A gas thermometer measures the temperature from the variation of pressure of a sample of gas. If the pressure measured at the melting point of lead is 2.20 times the pressure measured at the triple point of water, find the melting point of lead.
The density of water at 0°C is 0.998 g cm–3 and at 4°C is 1.000 g cm–1. Calculate the average coefficient of volume expansion of water in the temperature range of 0 to 4°C.
A steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at 20°C.
Find the longitudinal strain developed in the rod if the temperature rises to 50°C. Coefficient of linear expansion of steel = 1.2 × 10–5 °C–1.
Answer the following question.
What is thermal stress?
A clock pendulum having coefficient of linear expansion. α = 9 × 10-7/°C-1 has a period of 0.5 s at 20°C. If the clock is used in a climate, where the temperature is 30°C, how much time does the clock lose in each oscillation? (g = constant)
A metre scale made of a metal reads accurately at 25 °C. Suppose in an experiment an accuracy of 0.12 mm in 1 m is required, the range of temperature in which the experiment can be performed with this metre scale is ______.(coefficient of linear expansion of the metal is `20 xx 10^-6 / (°"C")`
A metal rod of cross-sectional area 3 × 10-6 m2 is suspended vertically from one end has a length 0.4 m at 100°C. Now the rod is cooled upto 0°C, but prevented from contracting by attaching a mass 'm' at the lower end. The value of 'm' is ______.
(Y = 1011 N/m2, coefficient of linear expansion = 10-5/K, g = 10m/s2)
A uniform metallic rod rotates about its perpendicular bisector with constant angular speed. If it is heated uniformly to raise its temperature slightly ______.
An aluminium sphere is dipped into water. Which of the following is true?
The radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ∆T so that its new temperature is T + ∆T. The increase in the volume of the sphere is approximately ______.
Find out the increase in moment of inertia I of a uniform rod (coefficient of linear expansion α) about its perpendicular bisector when its temperature is slightly increased by ∆T.
Calculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of 57°C is drunk. You can take body (tooth) temperature to be 37°C and α = 1.7 × 10–5/°C, bulk modulus for copper = 140 × 109 N/m2.
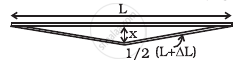
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
Length of steel rod so that it is 5 cm longer than the copper rod at all temperatures should be ______ cm.
(α for copper = 1.7 × 10-5/°C and α for steel = 1.1 × 10-5/°C)
A metal ball immersed in water weighs w1 at 0°C and w2 at 50°C. The coefficient of cubical expansion of metal is less than that of water. Then ______.
A glass flask is filled up to a mark with 50 cc of mercury at 18°C. If the flask and contents are heated to 38°C, how much mercury will be above the mark? (α for glass is 9 × 10-6/°C and coefficient of real expansion of mercury is 180 × 10-6/°C)
A clock with an iron pendulum keeps the correct time at 15°C. If the room temperature is 20°C, the error in seconds per day will be near ______.
(coefficient of linear expansion of iron is 1.2 × 10-5/°C)
A metal rod Y = 2 × 1012 dyne cm-2 of coefficient of linear expansion 1.6 × 10-5 per °C has its temperature raised by 20°C. The linear compressive stress to prevent the expansion of the rod is ______.
