Advertisements
Advertisements
Question
Convert the following in the polar form:
`(1+3i)/(1-2i)`
Solution
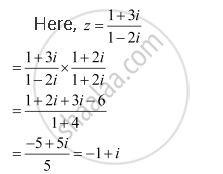
Let r cos θ = –1 and r sin θ = 1
On squaring and adding, we obtain
r2 (cos2 θ + sin2 θ) = 1 + 1
⇒r2 (cos2 θ + sin2 θ) = 2
⇒ r2 = 2 [cos2 θ + sin2 θ = 1]
APPEARS IN
RELATED QUESTIONS
Find the modulus and the argument of the complex number `z = – 1 – isqrt3`
Convert the given complex number in polar form: 1 – i
Convert the given complex number in polar form: – 1 + i
Convert the given complex number in polar form: – 1 – i
Convert the given complex number in polar form: –3
If the imaginary part of `(2z + 1)/(iz + 1)` is –2, then show that the locus of the point representing z in the argand plane is a straight line.
Let z1 and z2 be two complex numbers such that `barz_1 + ibarz_2` = 0 and arg(z1 z2) = π. Then find arg (z1).
Let z1 and z2 be two complex numbers such that |z1 + z2| = |z1| + |z2|. Then show that arg(z1) – arg(z2) = 0.
The locus of z satisfying arg(z) = `pi/3` is ______.
What is the polar form of the complex number (i25)3?
The amplitude of `sin pi/5 + i(1 - cos pi/5)` is ______.
Show that the complex number z, satisfying the condition arg`((z - 1)/(z + 1)) = pi/4` lies on a circle.
If arg(z – 1) = arg(z + 3i), then find x – 1 : y. where z = x + iy.
z1 and z2 are two complex numbers such that |z1| = |z2| and arg(z1) + arg(z2) = π, then show that z1 = `-barz_2`.
If for complex numbers z1 and z2, arg (z1) – arg (z2) = 0, then show that `|z_1 - z_2| = |z_1| - |z_2|`.
Write the complex number z = `(1 - i)/(cos pi/3 + i sin pi/3)` in polar form.
If z and w are two complex numbers such that |zw| = 1 and arg(z) – arg(w) = `pi/2`, then show that `barz`w = –i.
arg(z) + arg`barz (barz ≠ 0)` is ______.
If |z| = 4 and arg(z) = `(5pi)/6`, then z = ______.
State True or False for the following:
Let z1 and z2 be two complex numbers such that |z1 + z2| = |z1| + |z2|, then arg(z1 – z2) = 0.
Find z if |z| = 4 and arg(z) = `(5pi)/6`.
Find principal argument of `(1 + i sqrt(3))^2`.
|z1 + z2| = |z1| + |z2| is possible if ______.
The value of arg (x) when x < 0 is ______.
If arg(z) < 0, then arg(–z) – arg(z) = ______.
