Advertisements
Advertisements
Question
cosec x (log y) dy + x2y dx = 0
Solution
We have,
\[cosec\ x \left( \log y \right)dy + x^2 y dx = 0\]
\[ \Rightarrow \frac{\log y}{y}dy = - \frac{x^2}{cosec\ x}dx\]
\[ \Rightarrow \frac{\log y}{y}dy = - x^2 \sin x dx\]
Integrating both sides, we get
\[\int\frac{\log y}{y}dy = - \int x^2 \sin x dx . . . . . \left( 1 \right)\]
Putting log y = t
\[\frac{1}{y}dy = dt\]
Therefore, (1) becomes
\[\int t\ dt = - \int x^2 \sin x dx\]
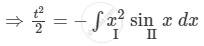
\[ \Rightarrow \frac{1}{2} \left[ \log y \right]^2 = - x^2 \int\sin x dx - \int\left( \frac{d}{dx}\left( x^2 \right)\int\sin x dx \right)dx\]
\[ \Rightarrow \frac{1}{2} \left[ \log y \right]^2 = x^2 \cos x + 2\int x \cos x dx\]

\[ \Rightarrow \frac{1}{2} \left[ \log y \right]^2 = x^2 \cos x - 2x\int\cos x dx + 2\int\left( \frac{d}{dx}\left( x \right)\int\cos x dx \right)dx\]
\[ \Rightarrow \frac{1}{2} \left[ \log y \right]^2 = x^2 \cos x - 2x \sin x - 2\cos x + C\]
\[ \Rightarrow \frac{1}{2} \left[ \log y \right]^2 = \left( x^2 - 2 \right)\cos x - 2x \sin x + C\]
\[ \Rightarrow \frac{1}{2} \left[ \log y \right]^2 + \left( 2 - x^2 \right)\cos x + 2x \sin x = C\]
APPEARS IN
RELATED QUESTIONS
Find the differential equation representing the family of curves v=A/r+ B, where A and B are arbitrary constants.
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
`x/a + y/b = 1`
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = a e3x + b e– 2x
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = e2x (a + bx)
Form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.
y = ex (a cos x + b sin x)
Find the particular solution of the differential equation (1 + e2x) dy + (1 + y2) ex dx = 0, given that y = 1 when x = 0.
Solve the differential equation `ye^(x/y) dx = (xe^(x/y) + y^2)dy, (y != 0)`
The general solution of a differential equation of the type `dx/dy + P_1 x = Q_1` is ______.
Find the differential equation representing the family of curves `y = ae^(bx + 5)`. where a and b are arbitrary constants.
Find the differential equation of all the circles which pass through the origin and whose centres lie on x-axis.
The equation of the curve satisfying the differential equation y (x + y3) dx = x (y3 − x) dy and passing through the point (1, 1) is
Show that y = C x + 2C2 is a solution of the differential equation \[2 \left( \frac{dy}{dx} \right)^2 + x\frac{dy}{dx} - y = 0.\]
Show that y2 − x2 − xy = a is a solution of the differential equation \[\left( x - 2y \right)\frac{dy}{dx} + 2x + y = 0.\]
Show that the differential equation of all parabolas which have their axes parallel to y-axis is \[\frac{d^3 y}{d x^3} = 0.\]
From x2 + y2 + 2ax + 2by + c = 0, derive a differential equation not containing a, b and c.
\[\frac{dy}{dx} = \frac{1}{x^2 + 4x + 5}\]
\[\frac{dy}{dx} - x \sin^2 x = \frac{1}{x \log x}\]
\[\frac{dy}{dx} = \sin^3 x \cos^2 x + x e^x\]
(1 − x2) dy + xy dx = xy2 dx
Find the general solution of the differential equation `"dy"/"dx" = y/x`.
Solve the differential equation:
cosec3 x dy − cosec y dx = 0
Find the general solution of the following differential equation:
`x (dy)/(dx) = y - xsin(y/x)`
The general solution of the differential equation `(dy)/(dx) + x/y` = 0 is
General solution of tan 5θ = cot 2θ is
Solution of the equation 3 tan(θ – 15) = tan(θ + 15) is
The general solution of the differential equation `(dy)/(dx) = e^(x + y)` is
The general solution of the differential equation `(ydx - xdy)/y` = 0
The general solution of the differential equation `x^xdy + (ye^x + 2x) dx` = 0
The general solution of the differential equation y dx – x dy = 0 is ______.
