Advertisements
Advertisements
Question
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- 352 children from a school went on a camping trip. Each tent had a group of 4 children.
a) How many children did each tent have? b) How many tents do they need? c) How many children in all are in the school?
Solution
| a) | How many children did each tent have? | |
| b) | How many tents do they need? | ✓ |
| c) | How many children in all are in the school? |
Option (a) is not a good choice because the number of children for each tent is already given.
Option (c) is not a good choice because the total number of children is already given.
APPEARS IN
RELATED QUESTIONS
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
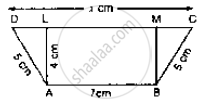
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
D is the mid-point of side BC of ΔABC and E is the mid-point of BD. if O is the mid-point
of AE, prove that ar (ΔBOE) = `1/8` ar (Δ ABC).
In the given figure, find the area of ΔGEF.
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find ar (ΔRAS)
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8cm and PQand BD intersect at O, then find area of ΔOPB.
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AErespectively. IF area of ΔABC is 16 cm2, find the area of ΔDEF.
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
In the given figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =

Find the area of a rectangle whose length and breadth are 25 m and 16 cm.
Find the area of a rectangle whose length = 8.5 m breadth = 5 m.
Find the area of a square, whose side is: 7.2 cm.
The side of a square is 3.6 cm; find its area.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is increased by 4 m?
Which has the bigger area - one of your footprints or the page of this book?
So the area of piece A = ________ square cm
In the same way, find the area of piece B.
This stamp has an area of 4 square cm. Guess how many such stamps will cover this big rectangle.

The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 meters of wire and tried to make different rectangles.
He made a 10 m × 40 m rectangle. Its area was 400 square meters. So he next made a 30 m × 20 m rectangle.
- What other rectangles can he make with 100 meters of wire? Discuss which of these rectangles will have the biggest area.
In the following figure, the area of parallelogram ABCD is ______.
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:
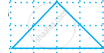
Find the area of the following figure by counting squares:

