Advertisements
Advertisements
Question
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- A shopkeeper has 50 boxes. There are 48 fruits in one box.
Tick the one question which matches with the given problem.
Explain why (a) and (c) are not good choices.a) How much will the shopkeeper pay in all? b) How many fruits are there in all? ✓ c) How many more boxes will he need?
Solution
- Option (a) is not a good choice because the price is not given in the story.
- Option (c) is not a good choice because the total number of boxes is given in the story.
APPEARS IN
RELATED QUESTIONS
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
If ABCD is a parallelogram, then prove that
𝑎𝑟 (Δ𝐴𝐵𝐷) = 𝑎𝑟 (Δ𝐵𝐶𝐷) = 𝑎𝑟 (Δ𝐴𝐵𝐶) = 𝑎𝑟 (Δ𝐴𝐶𝐷) = `1/2` 𝑎𝑟 (||𝑔𝑚 𝐴𝐵𝐶𝐷) .
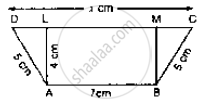
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

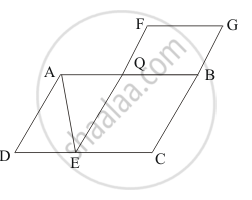
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
In the given figure, find the area of ΔGEF.
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ΔPBQ is 17cm2, find the area of ΔASR.
ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q such that CQ: QP = 3.1. If ar (ΔPBQ) = 10cm2, find the area of parallelogram ABCD.
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
Diagonal AC and BD of trapezium ABCD, in which AB || DC, intersect each other at O. The triangle which is equal in area of ΔAOD is
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
Find the area of a rectangle whose length and breadth are 25 m and 16 cm.
Find the area of a rectangle whose length = 15 cm breadth = 6.4 cm
Each side of a square is 7 m. If its each side be increased by 3 m, what will be the increase in its area.
Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is doubled?
Which has the bigger area - one of your footprints or the page of this book?
In the same way, find the area of piece B.
Karunya bought three fields.
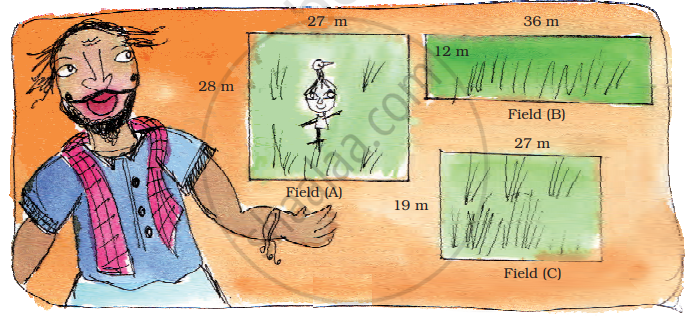
Find the area of all three fields.
- Field (A) ____________ square metre.
- Field (B) ____________ square metre.
- Field (C) ____________ square metre.
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- A shopkeeper has 204 eggs. He puts them in egg trays. Each tray has 12 eggs.
a) How many more eggs will he need? b) How many fresh eggs does he sell? c) How many egg trays does he need?
Area of a rectangle with length 5 cm and breadth 3 cm is ______.
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

