Advertisements
Advertisements
Question
If tan α = `1/7`, sin β = `1/sqrt10`. Prove that α + 2β = `pi/4` where 0 < α < `pi/2` and 0 < β < `pi/2`.
Solution
Given that tan α = `1/7`
We wish to find tan(α + 2β)
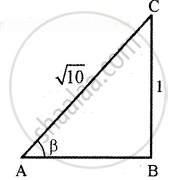
AB2 = AC2 - BC2
AB2 = 10 - 1
AB2 = 9
AB = 3
sin β = `1/sqrt10 = "Opposite side"/"Hypotenuse"`
tan β = `"Opposite side"/"Adjacent side" = 1/3` (Here β is an acute angle)
Now tan 2β = `(2 tan beta)/(1 - tan^2 beta)`
`= (2 (1/3))/(1 - (1/3)^2) = (2/3)/(8/9)`
`= 2/3 xx 9/8 = 3/4`
Consider tan (α + 2β) = `(tan alpha + tan 2 beta)/(1 - tan alpha tan 2beta)`
`= (1/7 + 3/4)/(1 - 1/7 xx 3/4)`
`= ((1 xx 4 + 3xx7)/28)/(1 - 3/28)`
`= (25/28)/(25/28)` = 1
tan (α + 2β) = `tan pi/4 (because tan pi/4 =1)`
∴ α + 2β = `pi/4`
APPEARS IN
RELATED QUESTIONS
Find the value of the following:
cot 75°
Find the value of the following:
sin 76° cos 16° – cos 76° sin 16°
Find the value of the following:
cos 70° cos 10° – sin 70° sin 10°
If cot α = `1/2`, sec β = `(-5)/3`, where π < α < `(3pi)/2 and pi/2` < β < π, find the value of tan(α + β). State the quadrant in which α + β terminates.
Prove that:
sin(A + 60°) + sin(A – 60°) = sin A.
If sin A = `12/13`, find sin 3A.
If sin α + sin β = a and cos α + cos β = b, then prove that cos(α – β) = `(a^2 + b^2 - 2)/2`
Find the value of tan `pi/8`.
Prove that `2 sin^2 (3pi)/4 + 2 cos^2 pi/4 + 2 sec^2 pi/3` = 10
If tan A = `1/2` and tan B = `1/3` then tan(2A + B) is equal to:
